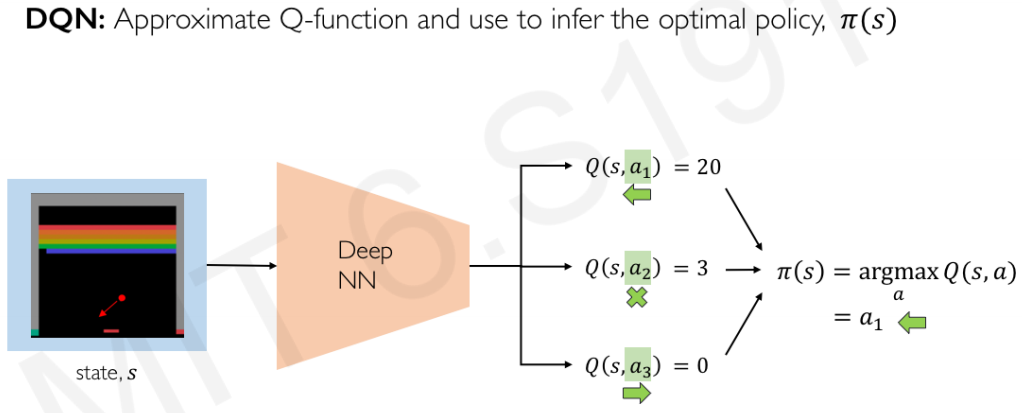
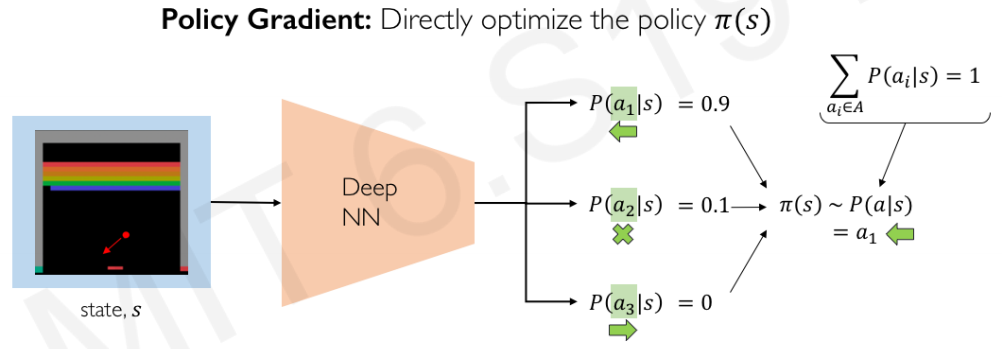
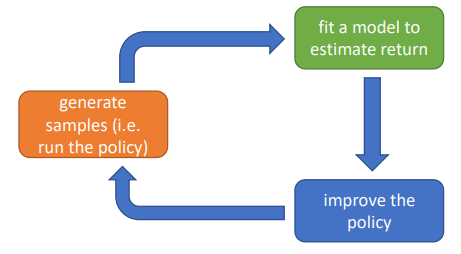
지난 포스트에서 살펴본 Q learning의 $optimal \; policy$란 cumulative reward를 maximize하는 것이므로 모든 state의 모든 action에 대한 quality value를 계산해두면 어느 state에서건 goal에 이르는 optimal (cumulative reward를 maximize하는) action을 구할 수 있다’로 요약할 수 있습니다.
하지만 real-world task에 적용하기에는 여러가지 문제가 있습니다. 우선 앞서 traditional Q learning의 단점으로 지적되었던 state-action space dimension 문제입니다. DQN으로 state space가 Atari game 정도로 확장된 task들에도 적용이 가능해지긴 했지만, 여전히 higher dimensional continuous state space에는 적용이 어렵고, 특히 Atari game과 달리 action space가 continuous한 경우는, discretization과 같은 트릭을 쓴다해도 scaling에 큰 제약이 있습니다. State 및 action space dimension이 늘어나면 Q network 자체 뿐만 아니라 성능 개선을 위해 추가했던 replay memory의 사이즈도 폭발적으로 증가하게 될 것입니다. 또한, exploration을 강화해서 학습을 ‘넓게’하기 위한 목적으로 추가한 $\epsilon$-greedy도 문제가 될 수 있는데요, optimal policy가 deterministic한 경우 작긴 하지만 계속해서 $\epsilon$만큼의 확률로 random action selection을 하게 되면 수렴 및 performance에 악영향이 있을 수 있습니다. 이러한 이유로 낭비스럽게 모든 state-action pair에 대한 Q value를 학습한 다음 거기서 optimal policy를 간접적으로 구해서 쓰는 방법 대신, input state에 대한 최적의 policy를 바로 학습하는 policy gradient method가 고안되었습니다.
* 이미지는 MIT 6.S191 lecture slide에서 가져왔습니다. 대신 유튜브 링크 공유합니다. 잘 준비된 intro 강의라서 이해가 쉬우니 꼭 보시길 권합니다.
MIT 6.S191에 대해 이야기한 김에, 이 강의에서 policy gradient의 학습 방법에 대해 자율주행차량의 예를 들면서 high-level로 굉장히 쉽게 설명한 부분이 있어서 보여드리고 시작하겠습니다. 우선 학습의 순서는 다음과 같습니다:
- Initialize the agent
- Run a policy until termination
- Record all states, actions, rewards
- Decrease probability of actions that resulted in low reward
- Increase probability of actions that resulted in high reward
그리고 그림으로 시나리오를 설명합니다:
| Episode#1 | Episode#2 | Episode#3 | Episode#4 |
|---|---|---|---|
 |
 |
 |
 |
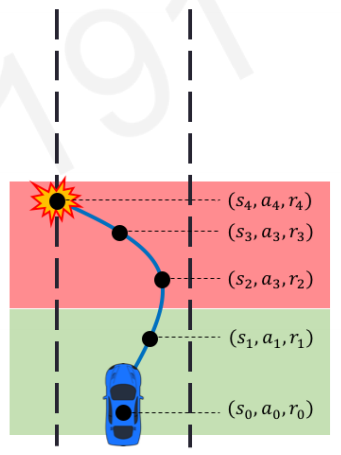
Episode#1
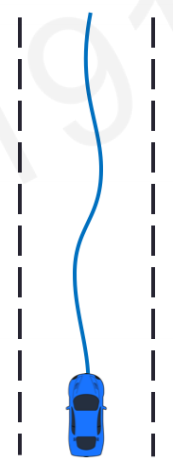
네트워크를 initialize하고 episode를 돌려봅니다. 첫 episode는 학습 전이기 때문에 금방 길가에 충돌하게 되었는데요, episode의 모든 step에 대해 state-action-reward tuple을 저장합니다. 이 중에서 crash라는 undesirable event에 기여도가 높은 충돌 전 몇 개의 step의 action의 선택 확률을 떨어뜨리는 쪽으로 네트워크를 학습하고, 처음 몇 step동안 어느정도 전진한 event에 기여도가 높은 초반 몇 step의 action에 대해서는 선택 확률을 높이는 쪽으로 네트워크를 학습합니다.
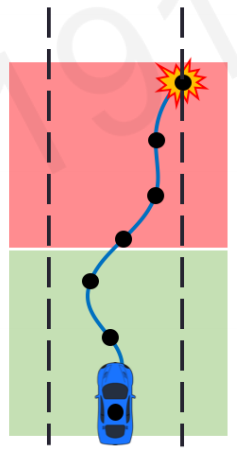
Episode#2
Episode#1에서의 학습을 통해 중간에 왼쪽으로 급하게 틀던 action이 선택되지 않으면서 앞으로 좀 더 가게 되었습니다만, 결국은 또 충돌이 생깁니다. Episode#1에서와 같은 방식으로 또 학습을 진행합니다.
Episode#3
이러한 학습을 반복할수록 자동차가 성공적으로 앞으로 나아가는 거리가 길어지게 됩니다.
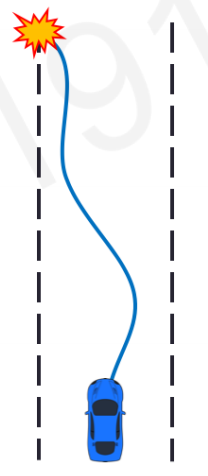
Episode#4
결국은 충돌하지 않고 goal까지 도달하게 됩니다.
지금부터 이러한 학습 방법이 어떻게 해서 도출되는지를 하나하나 살펴보면서 추적해보도록 하겠습니다.
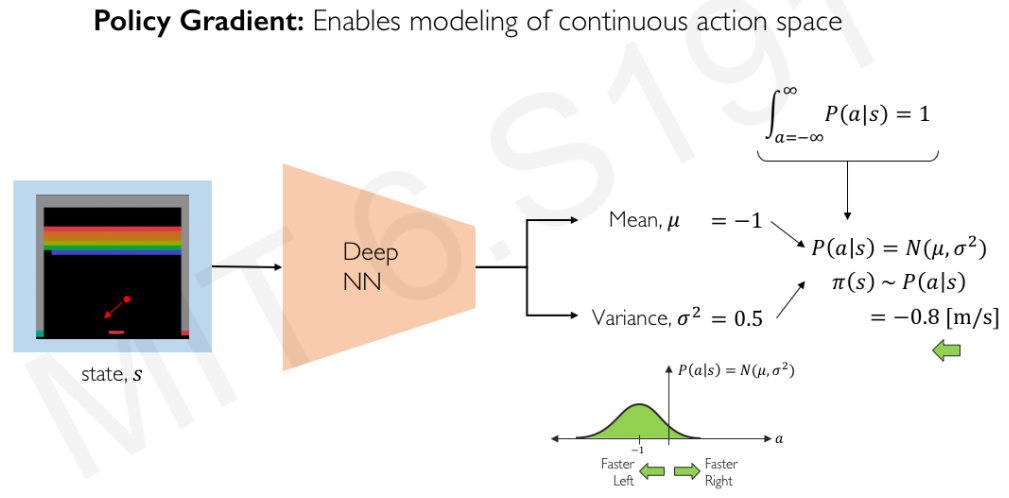
Policy gradient의 장점은 그 결과가 current state에 대한 각 action의 확률로 나오기 때문에 optimal policy가 deterministic한 경우라면 낮은 확률으로라도 randomness를 강제했던 value-based method의 $\epsilon$-greedy와 달리 stochastically deterministic하게 수렴하게 되며, optimal policy가 arbitrary한 경우에도 probability-based로 동작하기 때문에 대응이 가능하다는 점을 들 수 있습니다. 두 번째 경우를 좀 더 설명하자면, 예를들어 포커 게임을 학습한 경우 낮은 패를 쥐었을 때 Q learning과 같은 value-based 방법은 $argmax$로 도출한 optimal policy가 100% fold로 나오게 되는 반면 policy gradient는 가끔씩 블러핑을 할 수도 있습니다. 또한 앞서 설명한대로 모든 state-action space를 탐색하지 않고 probabilistically greedy하게 필요한 action을 선택하는 policy space만을 탐색하기 때문에 학습이 효과적입니다 (faster with fewer parameters). 또한 policy의 distribution이 Gaussian이라 가정하면 action space를 mean과 variance로 modeling할 수도 있게 됩니다. 즉, policy gradient를 DNN으로 구현했다면 이 output이 action들의 probability vector가 될 필요가 없고 action space를 나타내는 mean(zero-mean이라 가정하고 mean의 shift 값을 출력하면 되겠죠)과 variance만 출력해도 된다는 뜻입니다. 이렇게 되면 action space가 continuous하게 방대한 경우에도 modeling이 가능해집니다.
Value based 대비 policy gradient 방식의 단점은 environment의 작은 변화에도 성능이 영향을 받는다는 것을 들 수 있습니다. Value table을 학습한다는건 당장 optimal policy를 구하는 데는 쓰이지 않더라도 모든 state-action space의 lookahead table을 만들어둔다는 것이라고 생각할 수도 있는데요, 그렇기 때문에 environmental change에 어느정도 resilience를 가집니다. 하지만 current environment에서 optimal한 policy를 찾는데 최적화된 policy network는 작은 environmental change에도 학습을 새로 해야 합니다.
여타 RL과 마찬가지로 policy gradient에서도 expected reward를 maximize하는 것이 그 목표입니다.
$\qquad$ $J(\theta) = \mathbb{E}_{\pi}\left[ r(\tau) \right]$
$\qquad$ $\qquad$ $\pi$ or $\pi_{\theta}$: policy (parameterized by $\theta$)
$\qquad$ $\qquad$ $r(\tau)$: total reward for a given episode $\tau$
우리의 목표는 위의 $J$를 최대화하는 parameter $\theta$를 찾는 것이겠지요. 네트워크로 구현된 경우라면 저 $\theta$는 weights가 될 것입니다. Target $Q$와 estimated $Q$ 사이의 mean-quared error를 loss로 놓고 gradient descent search를 했던 Q learning과 달리, policy-based RL의 objective function은 expected reward이기 때문에 minimize하는 것이 아니라 maximize를 해야합니다. Update rule이 다음과 같이 되겠죠:
$\qquad$ $\theta_{t+1} = \theta_t + \alpha \nabla J(\theta_t)$
$\pi$가 policy의 probability로 표현되는 policy-based에서는 (특히 continous라면 더욱) expected reward를 다음과 같이 integral로 표현할 수 있습니다:
$\qquad$ $J(\theta) = \mathbb{E}_{\pi}\left[ r(\tau) \right] = \int \pi(\tau)r(\tau)$
$\qquad$ $\nabla J(\theta) = \nabla \mathbb{E}_{\pi}\left[ r(\tau) \right] = \nabla \int \pi(\tau)r(\tau)d\tau$
$\qquad$ $\qquad$ $= \int \nabla \pi(\tau)r(\tau)d\tau$
$\qquad$ $\qquad$ $= \int \pi(\tau) \nabla ln \; \pi(\tau) r(\tau)d\tau \quad (\because ln \; \pi(\tau) = \frac{1}{\pi(\tau)})$
$\qquad$ $\qquad$ $= \mathbb{E}_{\pi}\left[ r(\tau) \nabla ln \; \pi(\tau) \right]$
마지막 식을 글로 풀어쓰면 ‘expected reward의 미분값은 reward $\times$ (policy($\pi_{\theta}$)에 로그를 취한 값의 gradient)와 같다’ 인데요, 이것이 바로 Policy Gradient Theorem 입니다.
* Policy Gradient theorem의 증명은 여러 방식으로 가능한데요, 또다른 증명 한 가지를 링크로 대신합니다.
이렇게 policy gradient에 $ln$을 취한 값은 product($\prod$)로 표현되던 episode 내 policy를 sum으로 바꿔주고, $\theta$와 무관한 initial state의 probability 및 state transition probability term을 제거시켜 주어 derivative of expected reward를 episode 내의 각 step의 policy probability만으로 간소화 시켜주는 효과를 낳아, 드디어 policy의 미분값만으로 backpropagation을 이용해서 (그리고 reward 값과 곱해야죠) gradient의 contribution을 구할 수 있게 됩니다:
$\qquad$ $\pi_{\theta}(\tau) = \mathcal{P}(s_0) \prod^T_{t=1} \pi_{\theta}(a_t \mid s_t)p(s_{t+1}, r_{t+1} \mid s_t, a_t)$
$\qquad$ $ln \;\pi_{\theta}(\tau) = ln \; \mathcal{P}(s_0) + \sum^T_{t=1} ln \; \pi_{\theta}(a_t \mid s_t) + \sum^T_{t=1} ln \; p(s_{t+1}, r_{t+1} \mid s_t, a_t)$
이 과정 이후 남은 식은 다음과 같습니다:
$\qquad$ $\nabla \mathbb{E}_{\pi_{\theta}} \left[ r(\tau) \right] = \mathbb{E}_{\pi_{\theta}} \lbrack r(\tau) \left( \sum^T_{t=1} \nabla ln \; \pi_{\theta} (a_t \mid s_t) \right) \rbrack$
이제 $r(\tau)$를 $\sum$ 안에 넣으면 해당 step부터의 cumulative reward인 $G_t$로 바꾸어 표기할 수 있으며, REINFORCE 알고리즘의 최종 update rule이 완성됩니다:
$\qquad$ $\nabla \mathbb{E}_{\pi_{\theta}} \left[ r(\tau) \right] = \mathbb{E}_{\pi_{\theta}} \lbrack \left( \sum^T_{t=1} G_t \nabla ln \; \pi_{\theta} (a_t \mid s_t) \right) \rbrack \quad (\because G_t = \sum^T_{t=1} R_t)$
REINFORCE (Monte-Carlo Policy Gradient)
Pseudocode부터 보겠습니다:
«REINFORCE algorithm»
Initialize the policy parameter $\theta$ at random.
Do forever:
- Generate $N$ episodes ($\tau_1 \sim \tau_N$) following the policy. Each episode $\tau_i$ has the following sequence: $s_{i, 0}, a_{i, 0}, r_{i, 1}, s_{i, 1}, …, s_{i, T-1}, a_{i, T-1}, r_{i, T}, s_{i, T}$
- Evaluate the gradient using these samples:
$\qquad$ $\nabla_{\theta}J(\theta) \approx \frac{1}{N} \sum^N_{i=1} \left( \sum^{T_i - 1}_{t=0} G_{i, t} \nabla ln \; \pi_{\theta} (a_{i, t} \mid s_{i, t}) \right)$
$\qquad$ where $G_{i, t}$ for trajectory $\tau_i$ at time $t$ is defined as the cumulative rewards from the beginning of the episode:
$\qquad$ $G_{i, t} = \sum^{T_i - 1}_{t'=0} r(s_{i, t'}, a_{i, t'}))$
- $\theta \leftarrow \theta + \alpha \nabla_{\theta}J(\theta)$
이는 Monte-Carlo 방식의 REINFORCE로, on-policy로 동작하기 때문에 episode들을 수행한 뒤 update하는 방식이 아니라 매 step마다 online update를 하기 때문에 $i$ term이 추가되었습니다 (여전히 future reward는 online으로 알 방법이 없으니 일단 episode를 끝까지 돌려서 각 step의 reward를 구한 다음, 다시 해당 episode의 매 step을 복기하면서 step-wise gradient update를 하면 됩니다). 충분히 큰 $N$ 횟수만큼 돌리면 정답에 수렴하게 될 것이기 때문에 등호 대신에 $\approx$ 기호를 사용했습니다.
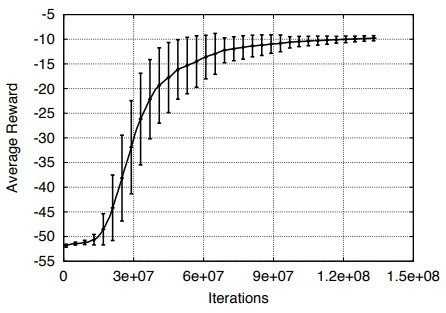
위와 같은 update rule을 가지는 vanilla REINFORCE는 policy가 probabilistic하게 결정되기 때문에 특정 episode의 특정 state에서 서로 다른 action을 선택할 가능성이 늘 있습니다. 그런데 optimal vs suboptimal policy에 대한 $G_t$값의 차이가 지나치게 들쭉날쭉하다면 (variance가 크다면), $G_t$가 update rule의 매 gradient에 곱해지는 값이기 때문에 학습이 수렴되는 것을 어렵게 만듭니다. 예를 들면 아래의 그래프처럼 수렴에 수많은 iteration이 필요하고 variance가 큰 것을 볼 수 있습니다 (David Silver의 RL Ch.7 강의자료이며, iteration 단위가 million임).이를 좀 완화하기 위해 cumulative reward ($G_t$)를 구할 때 discount rate ($\gamma$)를 추가하였지만 여전히 variance를 충분히 줄여주지는 못합니다. 이러한 variance 문제를 줄여주기 위한 몇 가지 방법이 고안되었습니다:
Causality (Reward-to-go)
앞서 $G_t$를 $t=0 \sim T$ ($T$: time of episode termination) 까지의 reward의 합으로 계산하였는데요, 이 cumulative reward는 'current state $s$에서 action $a$를 취할 때 받을 immediate reward 및 future reward의 총합'이기 때문에 과거에 이미 받은 reward를 현재의 cumulative reward에 더할 필요가 없습니다.
즉 $G_{i, t} = \sum^{T_i - 1}_{t'=0} r(s_{i, t'}, a_{i, t'})$가 $G_{i, t} = \sum^{T_i - 1}_{t'=t} r(s_{i, t'}, a_{i, t'})$ 로 바꿀 수 있으며, 이로 인해 전체적으로 gradient에 곱해지는 값의 magnitude를 떨어뜨려 variance 문제를 완화시킬 수 있습니다.
Discount rate
앞서 Q learning에서도 보셨듯이 future reward에 discount rate를 곱해서 $G_t$를 discounted cumulative reward로 만들 수 있으며, 이것 또한 variance를 줄여줍니다.
Causality 와 Discount rate trick을 적용한 gradient estimate은 다음과 같이 변경됩니다:
$\qquad$ $\nabla_{\theta}J(\theta) \approx \frac{1}{N} \sum^N_{i=1} \sum^{T_i - 1}_{t=0} \nabla_{\theta} ln \; \pi_{\theta} (a_{i, t} \mid s_{i, t}) \times \left( \sum^{T_i - 1}_{t'=t} \gamma^{t'-t}r(s_{i, t'}, a_{i, t'}) \right)$
Baseline
위의 policy gradient theorem은 reward에서 action($\theta$)에 dependent하지 않은 어떠한 식을 차감하더라도 상수화해서 소거가 가능하기 때문에 variance를 줄여주기 위한 arbitrary function을 넣어줄 수 있습니다. 모든 policy가 $\ge$ 0인 대부분의 경우 “좋은” policy든 “나쁜” policy든 reward를 증가시키게 되는데, 이에 비해 “나쁜” policy가 reward를 감소시키도록 하면 variance도 줄어들고 수렴도 쉬울 것입니다. 이같은 역할을 위한 function을 baseline 이라 하고, baseline 이 적용된 update rule은 다음과 같이 바뀝니다 (Causality 와 Discount rate 도 적용):
$\qquad$ $\nabla_{\theta}J(\theta) \approx \frac{1}{N} \sum^N_{i=1} \sum^{T_i - 1}_{t=0} \nabla_{\theta} ln \; \pi_{\theta} (a_{i, t} \mid s_{i, t}) \times \left( \sum^{T_i - 1}_{t'=t} \gamma^{t'-t}r(s_{i, t'}, a_{i, t'}) - b(s_t) \right)$
아무 function이나 baseline 으로 쓸 수는 있지만 몇 가지 대표적인 예는 다음과 같습니다:
- Constant baseline: 모든 episode $\tau$의 final reward의 평균을 baseline으로 차감
$\qquad$ $b = \mathbb{E} \lbrack R(\tau) \rbrack \approx \frac{1}{N} \sum^N_{i=1} R(\tau^{(i)})$
- Optimal Constant baseline: 수학적으로 variance ($Var \lbrack x \rbrack = E \lbrack x^2 \rbrack - E {\lbrack x \rbrack}^2$)를 최소화하는 값을 계산한 optimal 값이지만 성능 개선 정도에 비해 computational burden이 심해서 자주 사용되지는 않음
$\qquad$ $b = \frac{\sum_i (\nabla_{\theta} log \; P(\tau^{(i)}; \theta)^2)R(\tau^{(i)})}{\sum_i (\nabla_{\theta} log \; P(\tau^{(i)}); \theta)^2}$
- Time-dependent baseline: episode 기준으로 reward를 계산하여 averaging을 하는 것이 아니라, 각 episode 내의 모든 step(state-action pair)들에 대해 reward를 구해 평균을 낸 것으로, Causality (Reward-to-go) 적용 가능 (수식은 Causality 적용)
$\qquad$ $b_t = \frac{1}{N} \sum^N_{i=1} \sum^{T-1}_{t'=t} r(s_{i, t'}, a_{i, t'})$
- State-dependent expected return: episode나 step이 아니라 특정 state에 dependent한 reward (현재 policy에 의하면 state $t$에서 평균 얼마만큼의 reward가 예상되는가)를 계산
$\qquad$ $b(s_t) = \mathbb{E} \lbrack r_t + r_{t+1} + r_{t+2} + … + r_{T-1} \rbrack = V^{\pi}(s_t)$
위의 여러가지 baseline 중 ‘current state $s_t$에서 current policy $\pi_{\theta}$로 취할 수 있는 평균 future reward’를 말하는 state-dependent expected return $V^{\pi}(s_t)$은 각 state에서 특정 action을 취하는 것이 해당 state의 평균 future reward보다 얼마나 더 좋은가를 측정하여, 그 정도에 따라서 특정 action이 선택될 확률을 높이거나 낮출 수 있는 기준이 될 수 있기 때문에 arbitrary function을 baseline으로 삼는 것에 비해 보다 효과적이라 할 수 있습니다.
$V^{\pi}(s_t)$는 여러 다양한 function approximator를 사용해서 구현할 수 있습니다. 예를 들면 별도의 network를 구성하여 다음과 같이 Monte-Carlo 방식으로 구하는 것도 한 가지 방법이 될 수 있습니다:
- Initialize $V^{\pi}_{\phi_0}$ ($\phi$: regressor parameter)
- Collect episodes $\tau_1, \tau_2, …, \tau_N$
- Regress against reward from each episode:
$\phi_{i+1} \leftarrow argmin_{\phi} \frac{1}{N} \sum^N_{i=1} \sum^{T-1}_{t=0} \left( V^{\pi}_{\phi}(s_{i, t}) - (\sum^{T_i - 1}_{t'=t} r(s_{i, t'}, a_{i, t'})) \right)^2 $
Actor-Critic Method (A2C, A3C)
Baseline $b(s_t)$(우린 $V^{\pi}(s_t)$로 하기로 했죠)의 앞부분($\sum^{T_i - 1}_{t'=t} \gamma^{t'-t}r(s_{i, t'}, a_{i, t'})$)을 보시면 앞서 살펴본 Q learning의 Q value (given current policy $\pi$)와 동일하다는 것을 알 수 있습니다. 앞서 Q value는 network로 학습할 수 있다는 것을 보았으니 여기서도 Q estimate를 network로 구할 수 있습니다. Policy network의 parameter를 $\theta$로 쓰고 있으니, Q network의 parameter는 $\mathcal{w}$으로 놓고, Q 함수를 $Q_{\mathcal{w}}(s, a)$라고 하겠습니다 (더 정확하게는 $Q^{\pi_{\theta}}(s, a)$ 이라고도 쓸 수 있겠죠). 이 별도의 Q network의 학습도 on-policy로 진행합니다.
이제 Actor-Critic의 기본 구조가 모두 완성되었습니다. “Actor”와 “Critic” 역할을 하는 두 개의 network를 사용해서, “Critic”에 의해 계산된 approximate policy gradient로 “Actor”을 update하는 방식입니다. 즉, “Actor”는 given state의 policy distribution을 output하고, “Critic”은 “Actor”의 current policy를 평가하여 update의 방향 및 정도를 제공하는 역할을 하게 되는거죠. 이러한 역할 분담 때문에 이를 Actor-Critic method라고 부릅니다.
Actor-critic만 해도 여러 variants가 있는데요, 앞서 설명드린 것이 바로 A2C와 A3C에 사용되는 Advantage Actor-Critic 방법입니다. Advantage Actor-Critic에서 쓰이는 Advantage 함수는 이미 설명한대로 다음과 같이 $A(s, a) = Q(s, a) - V(s)$ Q와 V를 하나로 묶은 함수에 불과합니다 (지난 포스트의 dueling DQN에서 이야기한 Advantage term과 동일합니다). 여기서 Q 함수를 정의대로 다시 풀어서 써보면 $A(s, a) = r_{t+1} + \gamma V_{\mathcal{v}}(s_{t+1}) - V_{\mathcal{v}}(s_t)$ (변수가 바뀌었으니 parameter도 이번엔 $\mathcal{v}$로 바꿔서 표현)가 될 것이므로, 결국 Critic network는 $V(s_t)$만 output해서 $A(s, a)$를 계산할 수 있게 되는거죠. 이러한 Advantage function을 이용한 것이 A2C, 그리고 A2C network를 parallel하게 여러 개를 돌리면서 동일한 구조를 가진 global network를 asynchronous하게 업데이트하는 것이 A3C 입니다.
«Online Actor-Critic algorithm»
- Take action $a$ following $\pi_{\theta}(a \mid s)$, get $(s, a, s’, r)$
- Update $V_{\mathcal{v}}$ using target $r + \gamma V_{\mathcal{v}}(s’)$
- Evaluate $A(s, a) = r_{t+1} + \gamma V_{\mathcal{v}}(s_{t+1})$
- $\nabla_{\theta} J(\theta) \approx \nabla_{\theta} ln \; \pi_{\theta}A(s, a)$
- $\theta \leftarrow \theta + \alpha \nabla_{\theta} J(\theta)$
아래 그림과 같이 cyclic하게 동작하는 Actor와 Critic은 별개의 network 2개로 구현할 수도, 지난 포스트에서 본 duel network 1개로 구현할 수도 있습니다. 일반적으로 input이 simple해서 feature downsample이 간단한 경우에는 별개의 network로 구현해도 성능에 별 영향이 없으나, real image와 같이 high dimensional input이 들어오는 경우에는 두 network에서 동일한 feature selection 과정을 거치는 것이 낭비스럽고 수렴에도 영향이 있을 것이기 때문에 duel network 형태로 구현합니다.
Policy-gradient도 Actor-Critic variants를 포함하여 TRPO, PPO 등 수많은 variant들이 존재하지만, 기본적인 policy-based method의 동작방식 및 대표 알고리즘에 대해서는 살펴보았다고 생각되니 이것으로 마무리하고 다음으로 넘어가도록 하겠습니다. 원래 neuroevolution에 대해 이야기하려고 시작한 시리즈가 주변 설명에 시간이 너무 많이 소비되었네요. 취지대로 다음 포스트 부터는 Uber AI에서 진행된 (그리고 OpenAI에서도 연구된) neuroevolution에 대해 알아보도록 하겠습니다.