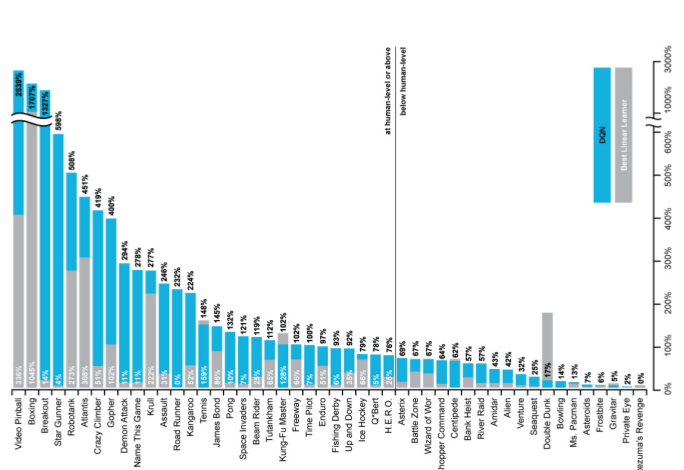
오랜만에 쓰네요.
엎어진 김에 쉬어간다고 traditional reinforcement learning (RL)에 대해 정리하고 넘어가도록 하겠습니다.
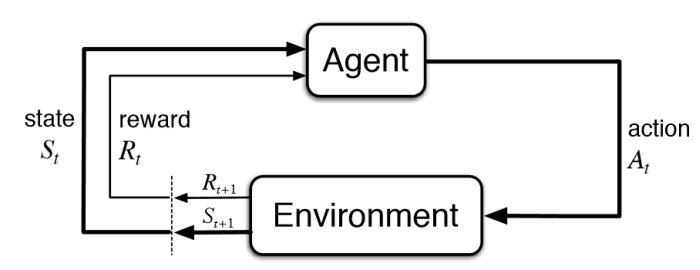
RL에 대해 조금이라도 찾아보신 분들이라면 agent가 environment로 action을 가하고, environment로부터 state와 reward를 받아오는 아래 그림이 매우 익숙하실 것입니다. 굳이 한 줄 쓰자면, environment로부터 time $t$의 current state $S_t$를 받은 agent가 이 state에서 가능한 action $A_t$를 수행하면 이 action에 따른 reward $R_{t+1}$을 받습니다. 이후 environment에서는 state를 $S_{t+1}$로 업데이트하고… 이 과정을 goal state가 발견될 때까지 반복하는 것입니다.
$S_0, A_0, R_1, S_1, A_1, R_2, S_2, A_2, R_3, …$
RL에서 풀고자 하는 문제는 이렇게 environment 안에서 sensing 및 acting을 하는 agent가 어떻게 하면 goal을 달성하기 위한 optimal한 action을 선택할 지를 학습하는 것입니다. 다시 말하면 goal을 달성하기까지 environment로부터 받는 reward를 maximize하기 위한 action 선택 전략, 즉 $optimal \; policy$를 학습하는 것이라고 할 수 있겠습니다. 그런데 이 reward (혹은 penalty)는 처음부터 모든 state에서 주어지는 것이 아닙니다. 체스와 같은 보드게임의 예를 들면 최종적으로 게임을 이겼는지의 여부에 따라 reward가 주어지는 것이지, 그 과정까지의 action에 대해서는 problem domain에 대한 어지간한 지식이 있지 않고서는 reward/penalty 값을 assign하기가 쉽지 않습니다. 현재의 action이 게임의 승패에 얼마나 영향을 미쳤는지를 거꾸로 추적하여 reward/penaly를 매겨야 하기 때문에 이러한 RL은 temporal credit assignment problem이라고도 볼 수 있습니다. Supervised classification과 빗대어 보자면 classification error gradient를 backpropagation을 통해 각 edge에 spatial하게 assign하여 weight update를 했던 것과 어떤 측면으로는 좀 비슷하게, RL은 이전의 action selection \(policy\)들의 ‘기여도’를 추정하여 temporal하게 각 policy의 reward를 update하는 것이죠.
$Optimal \; policy$를 찾기 위해 RL problem을 Markov Decision Process (MDP)로 formalize할 수 있습니다 (MDP에 대해 궁금하시면 여기 참고). MDP는 유한한 environment state space인 $S$, 각 state에서 가능한 action의 집합인 $A$ (state $s$에서 가능한 action들의 집합은 $A_s$로 표현), next state $s_{t+1}$이 current state $s_t$와, 당시의 action $a_t$에 의해 결정된다는 state transition function $s_{t+1}=\delta(s_t, a_t)$, 그리고 action $a_t$에 의해 state $s_t$가 $s_{t+1}$로 전이될 때 주어지는 reward function $r(s_t, a_t)$의 tuple <$S$, $A$, $\delta$, $r$>으로 나타낼 수 있고, 여기에 immediate vs delayed (future) reward 사이의 중요도를 구분함으로써 continuous task에서 reward가 무한대에 이르는 것을 막아주기 위한 discount factor $\gamma$를 추가한 <$S$, $A$, $\delta$, $r$, $\gamma$>의 5-tuple로 표현합니다.
Current state $s_t$로부터 다음 action $a_t$를 찾는 $policy$ ($\pi(s_t)=a_t$)를 $\pi : S \rightarrow A$로 정의합니다. 그리고 이 $\pi$에 의해 얻어지는 cumulative reward를 $V^{\pi}(s_t)$라고 하면 다음과 같은 정의가 성립합니다:
$\qquad$ $V^{\pi}(s_t) \equiv r_t + \gamma r_{t+1} + \gamma^2r_{t+2} + ... \equiv \sum^{\infty}_{i=0}\gamma^ir_{t+i}$
이제 $optimal \; policy$ $\pi^{\ast}$를 다음과 같이 정의할 수 있습니다:
$\qquad$ $\pi^{\ast} \equiv argmax_{\pi} V^{\pi}(s), (\forall s)$
위 정의는 ‘어떤 state에서 $optimal \; policy$란 해당 state로부터의 cumulative reward를 최대화하는 policy이다’라는 의미로 직관적입니다.
RL 솔루션은 크게 두 가지 방법론으로 나눌 수 있습니다. 하나는 학습을 통해 정확한 expected reward를 계산해내는 value-based method이고, 다른 하나는 취해야 하는 action을 학습하는 policy-based method 입니다. 두 번의 포스팅에 걸쳐 각각의 경우를 알아보겠습니다.
Q-Learning (Value-based)
위의 정의에 따라 given state $s$에서의 $optimal \; policy$를 다음과 같이 표현할 수 있습니다:
$\qquad$ $\pi^{\ast}(s) = argmax_{a} \left[r(s, a) + \gamma V^{\ast}(\delta(s, a)) \right]$
의미를 다시 보자면, ‘state $s$에서의 $optimal \; policy$란 이 state에서 어떤 action $a$를 취했을 때 “immediate reward $r(s, a)$와 그 action으로 도달하게 되는 후속 state $\delta(s, a)$의 maximum discounted cumulative reward $\gamma V^{\ast}(\delta(s, a))$의 합“이 최대가 되도록 하는 $policy$를 말한다’는 뜻입니다.
그런데 이 식은 $r(\cdot)$과 $\delta(\cdot)$에 대한 정보가 없이는 풀 수가 없습니다. 그래서 이 term들을 없애기 위해 고안된 것이 다음의 Q-function입니다:
$\qquad$ $Q(s, a) \equiv r(s, a) + \gamma V^{\ast}(\delta(s, a))$
이 Q-function은 이후 Q-estimate인 $\hat{Q}$ term을 이용하여 recursive한 식으로 만듭니다. 그리고 $\hat{Q}$가 $Q$로 수렴되도록 모든 state의 모든 action의 pair를 stochastically 수행한다는 것이 Q-learning입니다. 이 과정을 식으로 나타내면 다음과 같습니다:
$\qquad$ $\pi^{\ast}(s) = argmax_a Q(s, a)$
위 식은 $optimal \; policy$의 예전 식을 그냥 $Q$ term을 넣어서 rewrite한 것에 불과합니다.
$\qquad$ $V^{\ast}(s) = max_{a'}Q(s, a')$
이건 state $s$에서의 maximum discounted cumulative reward를 뜻하는 $V^{\ast}$를 식으로 쓴 것이고요.
이제 위의 Q-function을 다음과 같이 다시 쓸 수 있습니다:
$\qquad$ $Q(s, a) \equiv r(s, a) + \gamma max_{a'} Q(\delta(s, a), a')$
이 식을 estimated Q-function인 $\hat{Q}$로 바꿔쓰면 (next state는 $\delta(s, a) = s’$ 라고 쓰고요), 드디어 최종 식이 나옵니다:
$\qquad$ $\hat{Q}(s, a) \leftarrow r(s, a) + \gamma max_{a'} \hat{Q}(s', a')$
이제 아래의 pseudocode대로 충분히 여러차례 반복수행을 하게되면 Q-estimation이 real Q에 수렴하게 됩니다:
«Q learning algorithm»
For each $s, a$ initialize the table entry $\hat{Q}(s, a)$ to zero.
Observe the current state $s$
Do forever:
- Select an action $a$ and execute it
- Receive immediate reward $r$
- Observe the new state $s’$
- Update the table entry for $\hat{Q}(s, a)$ as follows:
$\qquad$ $\hat{Q}(s, a) \leftarrow r(s, a) + \gamma max_{a’} \hat{Q}(s’, a’)$ - $s \leftarrow s’$
Toy example을 어떻게 state diagram으로 만들고, 그에 따른 reward table을 만들고, Q table을 학습하는 지는 여기를 참고하시면 될 것 같습니다. 보다 더 일반적인 개념으로 temporal difference learning도 있고, Q learning에 randomness를 가미하는 $\epsilon$-greedy 등등의 방법들에 대해서는 뒤에 필요한 순간에 설명하도록 하고 지금은 생략합니다.
Deep Q Networks
간단하지만 powerful한 Q learning이 여러 toy problem에서 좋은 성능을 보였음에도 많이 사용될 수 없었던건 state와 action의 dimension이 커질수록 (특히 state) Q table의 dimension이 너무 커진다는 문제 때문입니다. 예를 들어 조악한 해상도를 가진 Atari 게임만 해도 Q table의 dimension이 7000x4(상하좌우로 움직이는 경우)나 되는데, camera 입력을 받는 자율주행 자동차 같은건 테이블 크기가 엄청나겠지요. Reward는 상대적으로 매우 sparse 해 질 것이고, 이걸 다 채우도록 학습을 하려면 엄청나게 많은 episode (또는 trajectory이나 rollout이라고 부름)가 필요할 것입니다. 한 마디로 불가능합니다.
이후 DNN이 high-dimensional real-world problem들을 성공적으로 해결하게 되고, Q learning에도 DNN 방법론을 접목하게 된 것이 Deep Q Networks (DQN) 입니다. DQN은 state를 입력하면 각 possible action에 대한 Q value들이 출력되는 DNN을 학습하여 기존의 Q table을 대체하였습니다.
Experience Replay
Q learning이 current episode의 연속적인 state-action pair에 대해 매번 Q table을 업데이트하는 방식이다보니 DQN도 episode가 진행되는 동안 계속해서 weight update를 하게 되는데, 이러면 매 episode의 sequence에 대해 DQN이 overfit되는 문제가 발생합니다. 이러한 consecutive sample 사이의 correlation을 없애기 위해 Experience Replay 라는 기법이 사용됩니다. Experience Replay 는 DQN을 on-policy로 업데이트하지 않고, 매번 consecutive하게 발생하는 experience를 별도의 replay memory에 저장해 두었다가 나중에 off-policy 방식으로 random하게 추출하면서 DQN을 업데이트하는 기법입니다. 이를 이용하면 consecutive expericne의 correlation도 줄일 수 있을 뿐더러, 한 experience가 DQN을 한 번 업데이트하고 사라져버리는 것이 아니라 재활용될 수 있고, mini-batch를 사용한 학습 속도 개선에도 기여할 수 있다는 부가적인 장점도 가지고 있습니다.
$\epsilon$-Greedy
$\epsilon$-greedy는 DQN에만 해당하는 것은 아니고 traditional Q learning에 적용되는 방법으로, Q learning이 greedy한 방식으로 exploitation에만 집중하는 것을 막기 위해 $\epsilon$ 만큼의 확률로 action을 random하게 선택하도록 하는 방법입니다. 알고리즘 수렴을 위해 $\epsilon$은 iteration을 더해가면서 줄여나가게끔 디자인합니다.
«Deep Q learning algorithm (w/ Experience Replay)»
Initialize replay memory $\mathcal{D}$ to capacity $N$
Initialize action-value function $Q$ with random weights
for episode = 1, $M$ do
$\qquad$ Initialize sequence $s_1 = \lbrace x_1 \rbrace$ and preprocessed sequenced $\phi_1 = \phi(s_1)$
$\qquad$ for $t=1, T$ do
$\qquad$ $\qquad$ With probability $\epsilon$ select a random action $a_t$
$\qquad$ $\qquad$ otherwise select $a_t = max_a Q^{\ast}(\phi(s_t), a; \theta)$
$\qquad$ $\qquad$ Execute action $a_t$ in emulator and observe reward $r_t$ and image $x_{t+1}$
$\qquad$ $\qquad$ Set $s_{t+1} = s_t, a_t, x_{t+1}$ and preprocess $\phi_{t+1} = \phi(s_{t+1})$
$\qquad$ $\qquad$ Store transition ($\phi_t, a_t, r_t, \phi_{t+1}$) in $\mathcal{D}$
$\qquad$ $\qquad$ Sample random minibatch of transitions ($\phi_j, a_j, r_j, \phi_{j+1}$)
$\qquad$ $\qquad$ Set $y_j = r_j$ for terminal $\phi_{j+1}$
$\qquad$ $\qquad$ Set $y_j = r_j + \gamma max_{a’} Q(\phi_{j+1}, a’; \theta)$ for non-terminal $\phi_{j+1}$
$\qquad$ $\qquad$ Perform a gradient descent step on ${(y_j - Q(\phi_j, a_j; \theta))}^2$
$\qquad$ endfor
endfor
맨 뒷부분의 gradient descent step은 결국 target (current) Q와 estimated Q 사이의 mean-squared error를 구한 것이라고 보셔도 무방합니다.
...
loss = self.MSE_loss(curr_Q, expected_Q.detach())
...
DQN variant들을 몇 개 소개하고 DQN을 마무리할까 합니다.
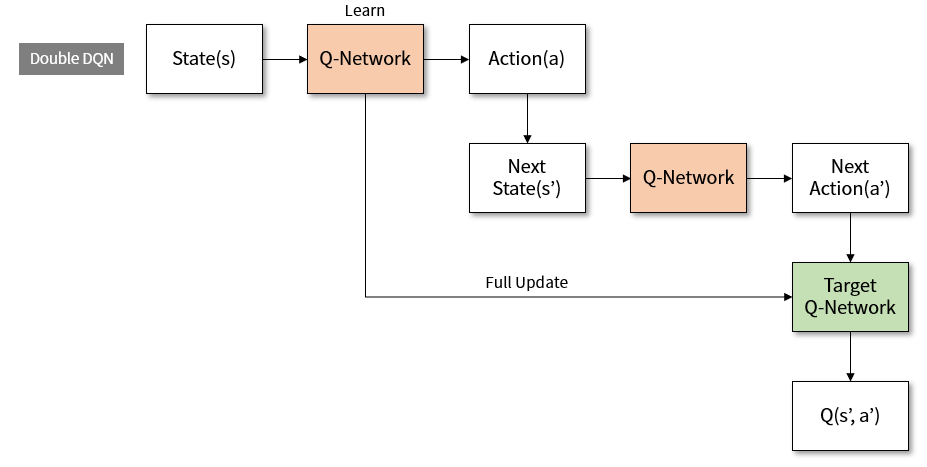
Double DQN (DDQN)
Q learning은 current state에 대해 Q table의 current estimation ($\hat{Q}$)에서 reward를 maximize하는 action을 선택하고, 그 max reward를 decay시켜 next Q를 update했습니다:
$\qquad$ $\hat{Q}(s, a) \leftarrow r(s, a) + \gamma max_{a'} \hat{Q}(s', a')$
DQN도 마찬가지였죠:
$\qquad$ Select $a_t = max_a Q^{\ast}(\phi(s_t), a; \theta)$
$\qquad$ $…$
$\qquad$ Perform a gradient descent step on ${(y_j - Q(\phi_j, a_j; \theta))}^2$
Target Network
우변의 estimation을 가지고 좌변의 target을 update하는 방식인데 $\hat{Q}$ term이 양변에 동일하게 들어가 있기 때문에, 매번 target이 update 될때마다 estimate의 값이 oscillate하게 되어서 $\hat{Q}$가 수렴하기 어려운 문제가 생깁니다. 그래서 별도의 target Q table (DQN의 경우에는 별도의 target Q network이 되겠죠)을 두고 여기서 next action과 reward를 뽑아내며, target network는 간헐적으로 (원래 Q network보다 드물게) 업데이트를 함으로써 Q network 수렴을 돕는다는 개념입니다. 간헐적으로 target Q network를 primary Q network로 reset시켜주는 방식도 있고, Polyak averaging ($\theta’ \leftarrow \tau \theta + (1-\tau)\theta’$, $\tau$: averaging rate)을 써서 미세하게 primary network와 target network의 차이를 줄이는 방향으로 target을 학습시키는 방식도 있습니다 (Soft Update).
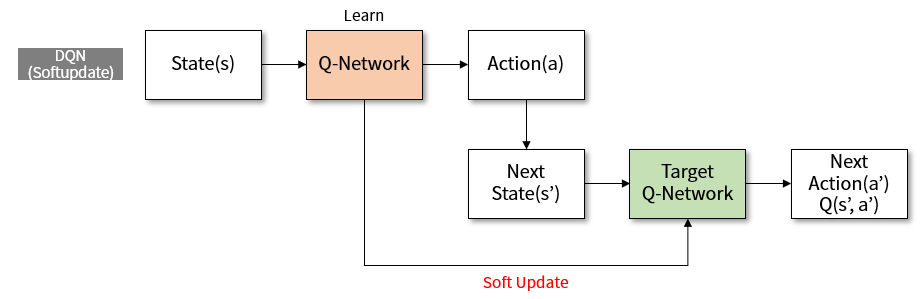
이 방식은 ‘모든 state가 관찰 가능하고, 모든 state에 대한 모든 action이 수행 가능한’ perfect environment에서라면 그다지 문제가 되지 않을 수도 있으나, 실제 학습 상황에서는 sensory값이 누락된다거나 environment에 변화가 생긴다거나 $\epsilon$-greedy처럼 non-deterministic하게 action을 수행하게 되는 noisy한 environment일 경우가 많습니다. Perfect environment라면 stochastic하게 optimal Q value로 수렴이 될 가능성이 높지만, 그렇지 않은 경우 Q table의 값이 몇몇 경우의 잘못 계산된 $max \hat{Q}$ 값에 의해 suboptimal하게 수렴되는 경우가 발생할 수 있습니다. 특히 overestimation의 우려가 크다고 밝혀졌는데, 이를 방지하기 위해 action selection은 primary Q network에서 하되, 그 action으로 인한 reward는 target Q network에서 가져오는 DDQN 방식이 고안되었습니다.
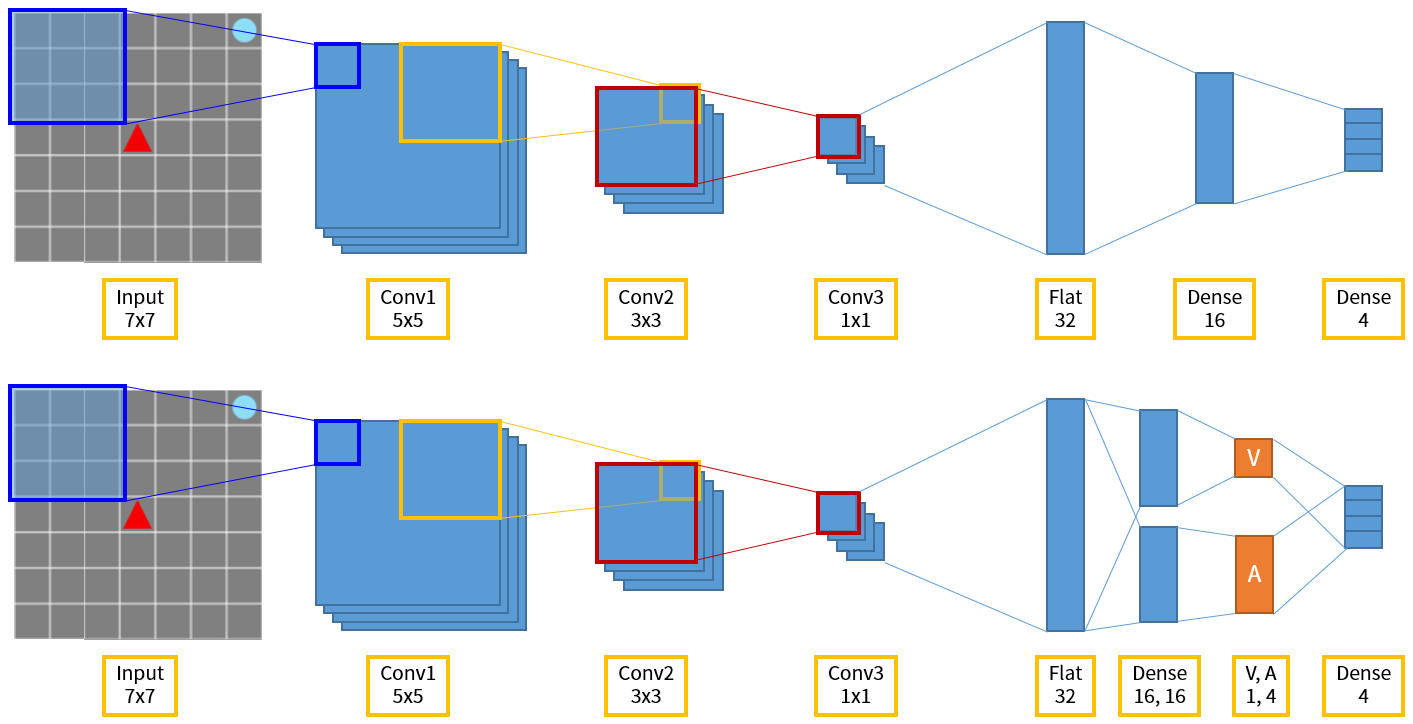
Dueling DQN
Dueling DQN은 network가 $Q(s, a)$를 $V(s)$와 $A(s, a)$라는 intermediate result (value)를 뽑아내게끔 분리하고, 이 값을 다시 합쳐서 $Q(s, a)$를 획득하는 방법입니다. $V(s)$는 앞서 보았던대로 state $s$의 value function이고, 새로 도입된 $A(s, a)$는 state $s$에서 action $a$를 취했을 때의 advantage를 나타내는 term입니다. 기존의 $Q(s, a)$가 이미 state $s$에서 action $a$를 취할 때의 value를 나타내는데 이걸 굳이 두 term으로 나누어 뽑아낸 까닭은, 어떤 task는 모든 state에서 action을 choice할 필요가 없기 때문에 state 정보와 action selection을 하나로 묶은 $Q$ term을 한꺼번에 학습하는 것이 불필요하게 느리고 복잡할 수가 있기 때문입니다. 또한 state와 action과의 tight correlation을 분리해서 action 자체의 general한 학습이 가능하다는 점도 장점이라 할 수 있습니다.
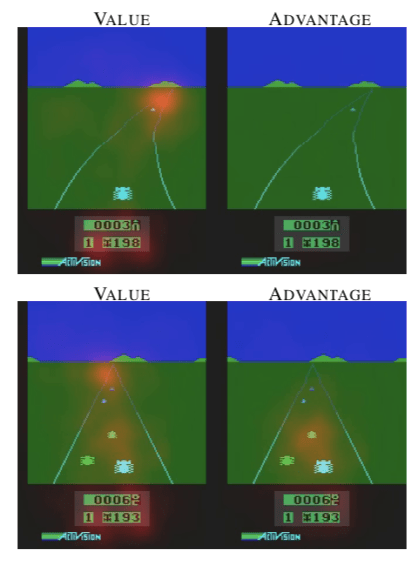
아래 그림은 다른 차량들을 추월해서 goal에 도달해야 하는 Enduro라는 Atari 게임인데요, 윗쪽 그림의 경우 network의 value stream은 action과 크게 관계없는 long-term goal인 road ahead 부분과 현재 score display 부분에 heatmap이 highlight된 반면, 다른 자동차가 주위에 없는 현재 상태에서 별다른 action이 필요없기 때문에 network의 action stream은 highlight된 부분이 없습니다. 하지만 state가 변해 주위에 차량이 접근하게 되어 개개의 action이 중요해진 아래쪽 그림의 경우에는 action stream이 가까운 차량에 highlight를 하는 것을 알 수 있습니다.
Combine된 $Q$ 값으로 $V$와 $A$ stream을 학습시키기 위해서는 $Q$ 값에 대한 각 stream의 contribution을 구분해야 하는 문제가 생기는데요 (problem of identifiability), average advantage를 사용하여 이 문제를 해결하였습니다. $Q$와 $V$, $A$의 관계식은 다음과 같습니다:
$\qquad$ $Q(s, a) = V(s) + \left( A(s, a) - \frac{1}{\mid A \mid}\sum_a A(s, a) \right)$
이 외에도 Noisy DQN, DQN with Prioritized Replay 등의 다양한 variant들이 있고, 여러 task를 동일한 parameter (learning rate)로 학습하고 성능을 높이기 위해 각 task의 reward를 scale해주는 Clipping Rewards 나 computational cost을 낮추어 더 많은 experience를 확보하기 위한 Frame Skipping 와 같은 트릭들 있습니다만, 모두 다룰 수는 없어서 여기까지로 DQN에 대한 소개를 마무리합니다. Traditional Q learning이 DNN과 결합하여 많은 task에서 superhuman performance를 보이면서 RL의 가능성을 다시금 열어주었으나, replay memory requirement 때문에 state dimension이 제한적인 경우에만 적용이 가능하다는 등 아직 보편적인 real-world problem에 적용하기에는 문제점도 가지고 있습니다. 다음 포스트에서는 이런 문제들을 해결해준 policy-based method에 대해 다루도록 하겠습니다.