지난 포스트에 attention mechanism이 다양한 task에 사용될 수 있다는 것을 보았습니다. 많은 연구자들의 관심이 쏠리자 결국 attention mechanism을 보다 더 다양한 task에 쉽게 사용하기 위한 generalization이 이루어지게 되고, 이렇게 일반화된 attention structure는 후에 다양한 network에 attention layer로 쉽게 넣어서 사용할 수 있게 됩니다. 이를 위해 지금까지 사용했던 notation을 재정의해보겠습니다. Attention layer는 말 그대로 ‘어느 input에 얼만큼씩 attend 해야 하는지’를 말해주는 layer이기 때문에, 지난 포스트에서의 seq-to-seq w/ attention 모델로 보면 encoder 부분만 구현한 것이라고 보시면 될 것 같습니다:
Attention Layer
Inputs:
- Query vector: $q$
- shape: $D_Q$ (dimensionality), 지난 설명에서는 decoder hidden vector $S_i$
- Input vectors: $X$
- shape: $N_X\times D_Q$, 지난 설명에서의 encoder hidden vector $H$
- Similarity function:
- $f_{att}$
Computation:
- Similarities: $e$
- shape: $N_X$
- $e_i = f_{att}(q, X_i)$
- Attention weights: $a = softmax(e)$
- shape: $N_X$
- Output vector: $y = \sum_{i}a_i X_i$
- shape: $D_X$
가장 먼저 similarity function이 generalize 됩니다. 초기 attention mechanism에서는 $f_{att}$를 network layer로 학습하였는데, 이를 학습 없이 훨씬 효율적인 dot product로 계산해도 비슷한 성능을 보인다는 점이 밝혀졌습니다. 이 dot product high dimensional input에 대해 너무 큰 값이 나온다는 단점, dot product 결과의 kurtosis가 너무 높은 경우 대부분의 softmax probability가 0이 되어버려서 gradient 또한 0이 되어버려서 vanishing gradient problem이 발생하여 학습이 매우 어려워진다는 단점이 있기 때문에, 이 dot product를 $sqrt(dim(q)=D_Q)$로 나눈 scaled dot product로 추가 개선됩니다.
다음 단계의 generalization은 multiple query vector를 사용하는 것입니다. 이전까지는 decoder time step마다 하나의 query vector ($q$, 예전의 $s_i$)를 사용하여 input state ($X$, 예전의 $H$)에 대한 하나씩의 similarity score를 구했는데요, 이제 모든 decoder state에 대한 모든 input vector들의 가중치를 한번에 계산하자는 것입니다. 앞서 similarity function을 scaled dot product로 generalize를 해 두었으니, 이제 similarity score를 구하는 것은 $Q$ (set of $q$)와 $X$의 matrix multiplication (MatMul)으로 간단히 구할 수 있습니다. 이렇게 구해진 similarity score에 한 방향으로 softmax를 적용하면 attention weight를 구할 수 있고, 이것과 input vector와 linear combination을 통해 encoder의 output vector를, 역시 한 번에 구할 수 있습니다.
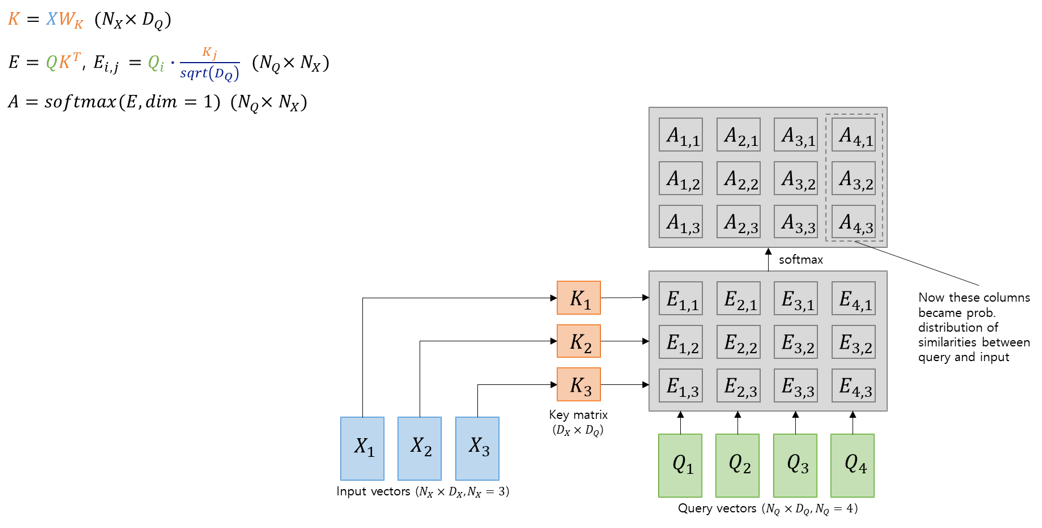
지금까지 input vector를 보면 두 가지 목적으로 사용된 것을 알 수 있는데요, 하나는 query vector와 비교하여 attention weight를 계산하기 위한 것이고 다른 하나는 이 attention weight와 결합하여 output vector를 만들기 위한 것입니다. 두 기능을 분리시켜 별도의 set of weights를 학습하게 한다면 모델 (layer)의 flexibility가 좋아질 것이라는 아이디어로, $key$와 $value$의 개념이 등장합니다. Similarity (attention weight)를 계산하기 위해 input vector에 key matrix $W_k$를 곱하여 key vector $K$를 구하고, 이걸 이용해서 similarity 계산을 합니다. $Softmax$를 거쳐 normalized probability distribution인 attention weight를 구한 다음, output vector를 계산할 때에는 input vector에 value matrix $W_v$를 굽한 value vector $V$를 구해서 attention weight와 곱해 output을 만들어냅니다.
여기까지 결과를 그림으로 보면 다음과 같습니다:
Initial state (input vector와 query vector만 있는 상태)
Key vector를 이용한 similarity 계산
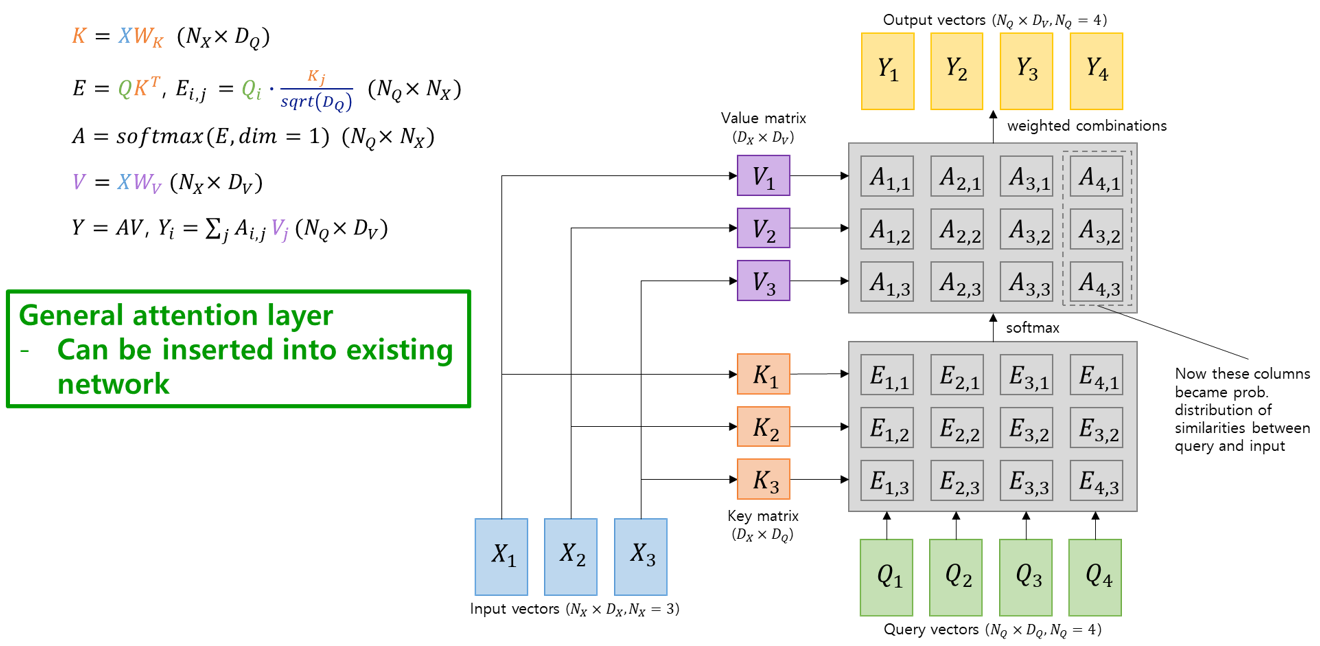
Value vector를 이용한 output 계산
이제 다른 network에 plug-in 해서 사용할 수 있는 general한 형태의 attention layer가 완성되었습니다. 최종 결과물을 output하기 위한 부분(decoder)에서 query vector를 만들어서, input vector와 잘 조합하여 해당 output이 input의 어떤 부분에 focusing을 할 지를 학습하는 방법이죠. 그런데 이렇게 query vector를 다른 부분에서 가져오지 말고, ‘input vector만 입력으로 받고, 여기에 뭔가 matrix 연산을 시켜서 input vector가 query vector를 predict하게끔 만들어 버리자’는 아이디어를 적용한 논문이 있었으니 그게 바로 “Attention is all you need”의 self-attention 입니다. 왜 ‘self’ attention인지도 감이 좀 오시죠?
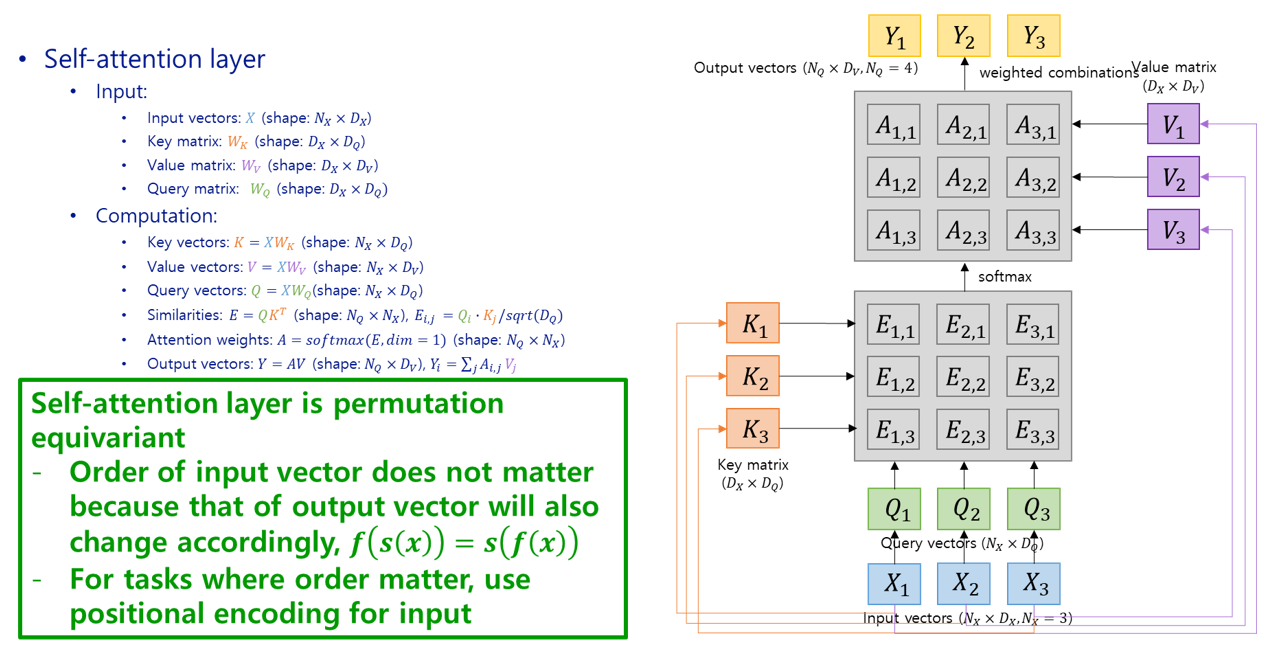
조금 전 generalization에서 key matrix와 value matrix를 쓴 것과 마찬가지로 query matrix를 사용하여 input vector와 곱해 query vector를 만들어 내고, 이후부터는 별도의 query vector가 있었던 때와 똑같이 동작하면 됩니다:
Self-attention layer
이 self-attention layer는 input vector의 순서가 바뀌면 output vector도 똑같이 순서가 바뀌도록 출력하는 굉장히 general한 network로, input order랑 상관없이 동작하는 ‘permutation equivariant’한 ($f(s(x)) = s(f(x))$) 모듈입니다. 그렇기 때문에 번역과 같이 input의 sequence가 중요한 task의 경우에는 input vector에 positional encoding을 붙여서 집어넣으면 됩니다.
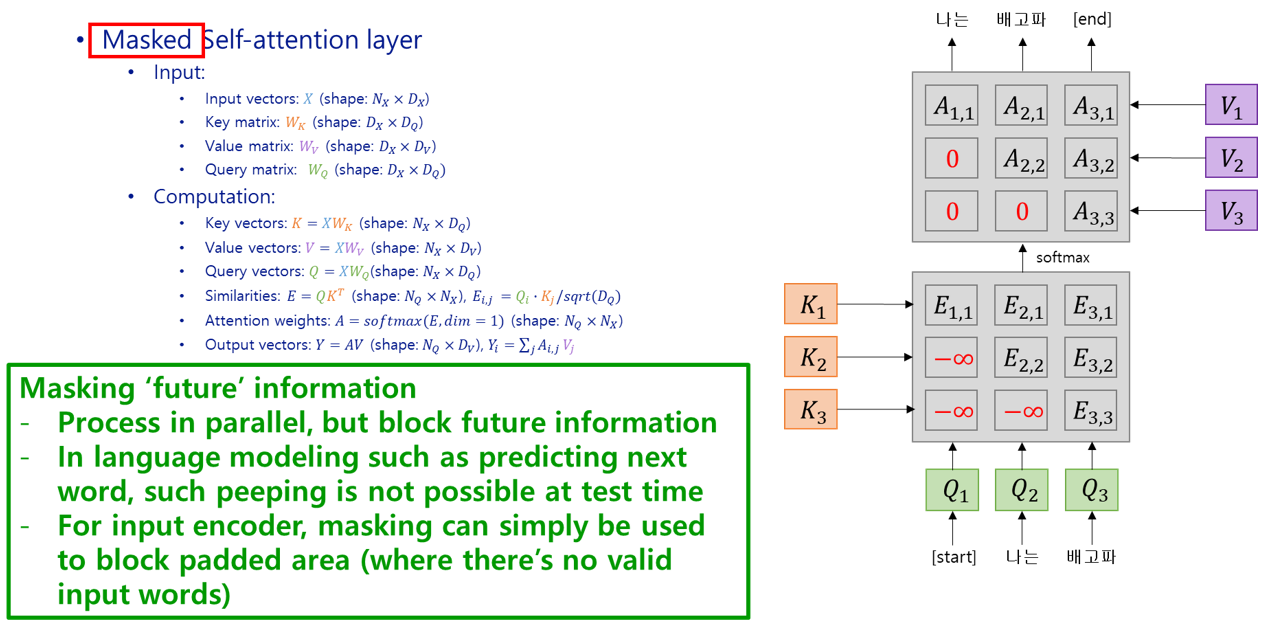
때로는 task에 따라 network가 previous input만 볼 수 있게 제한해야 하는 경우도 있습니다. 예를 들면 ‘지금까지의 text로 다음 word 맞추기’ 이런 task에서는 input vector가 full sentence가 들어오는 것이 아니라, word by word로 들어오고 network는 current and all previous input만을 가지고 next word를 예측할 것입니다. RNN에서는 input이 하나씩 순서대로 들어오기 때문에 구조적으로 이런 제약이 걸릴 수 밖에 없었는데요, attention layer는 input을 통으로 집어넣어도 동작하고, 순서가 있는 input도 positional encoding을 붙여서 통으로 집어넣으면 동작합니다. Positional encoding이 붙어있다면 input 순서를 뒤죽박죽으로 집어넣어도 ordered output을 뽑아낼 수도 있겠죠. 이런 경우에 ‘future’ input이 모델에 노출되는 것을 막기 위해 mask를 사용할 수 있습니다. 방법은 alignment score의 future input 부분을 $-{\infty}$로 넣어주어 softmax 계산 후 해당 부분의 attention weight가 0이 되게 만들면 됩니다. 그림으로 설명하죠:
Masked self-attention layer
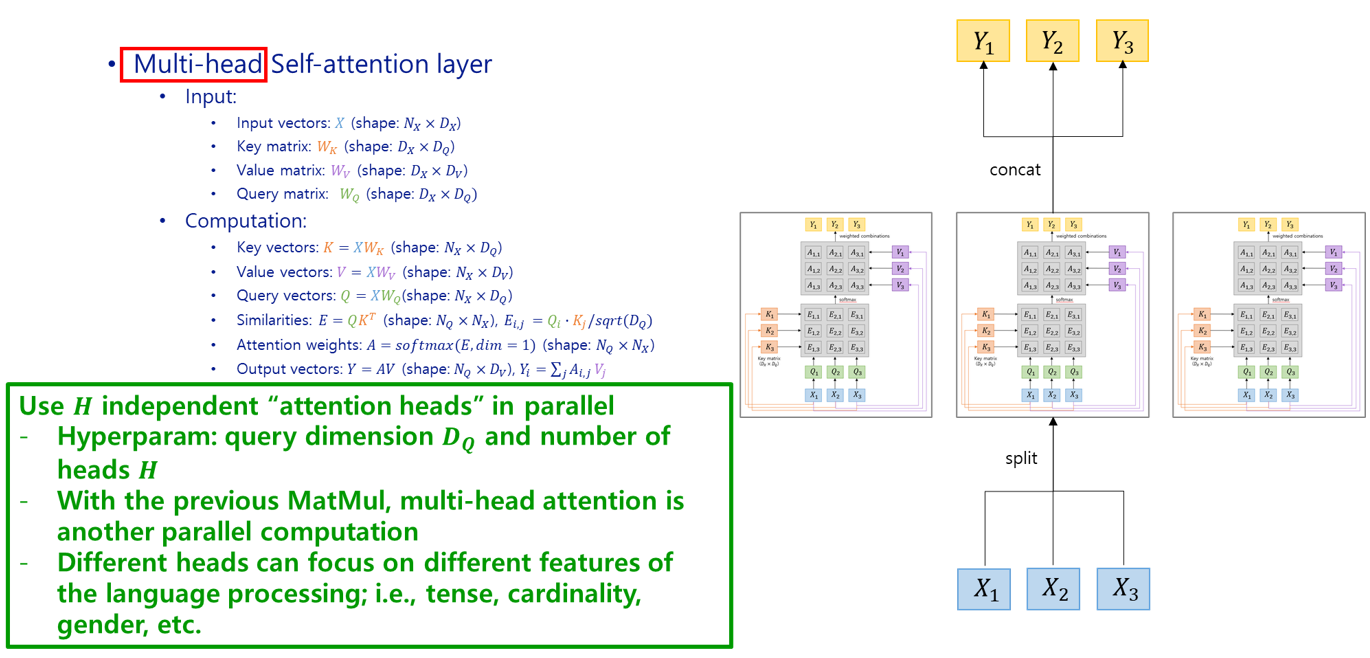
Self-attention layer 여러개를 parallel하게 배치하여 동시에 사용할 수도 있습니다. 예를 들면 language processing의 경우에 여러 self-attention layer가 각각 시제, 성/수, 단/복수 등의 문법적인 요소에 집중하게끔 하여 보다 정확한 output을 만들어 낼 수 있습니다. 이렇게 여러 self-attention layer를 parallel하게 사용하는 것을 multihead self-attention layer라고 합니다:
Multihead self-attention layer
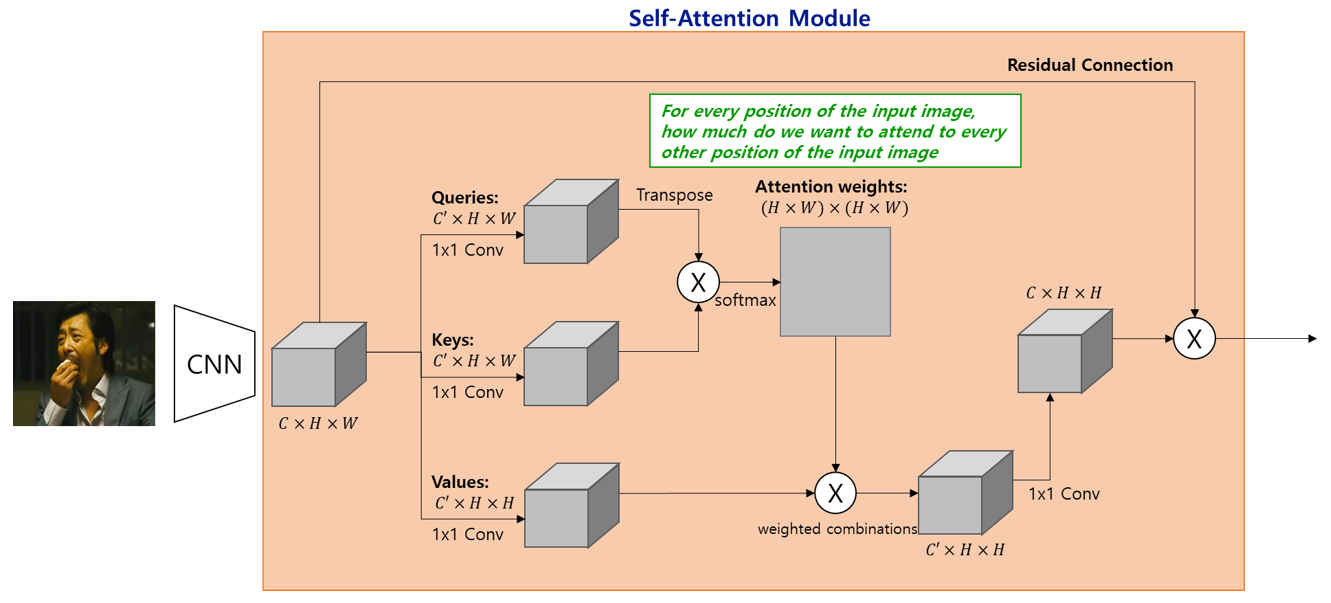
Set of vector를 input으로 하는 self-attention layer가 기존 network와 결합되어 사용되는 예를 보도록 하겠습니다. CNN과 함께 사용될 때이며, residual connection (skip connection)이 추가되어있습니다.:
Self-attention with CNN
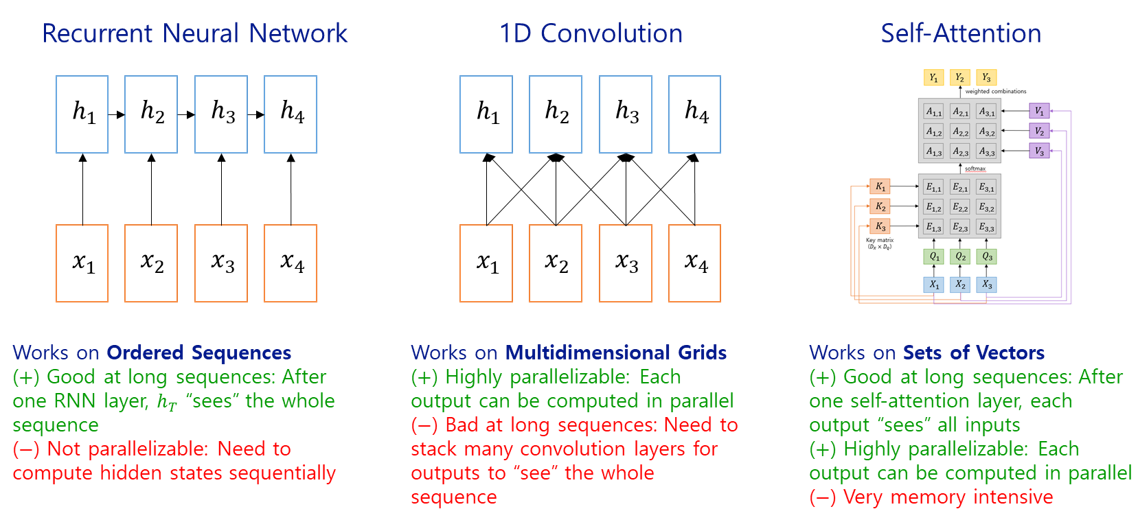
Sequence input을 처리하는 세 가지 primitive (RNN, 1D Conv, Self-attention)들을 비교해보면, RNN은 긴 sequence도 처리가 가능한 반면 parallel processing이 불가하여 high-end hardware의 잇점을 살리지 못한다는 단점이 있고, 1D convolution kernel을 sliding window 방식으로 적용하는 방법은 길이가 긴 sequence의 경우에 그만큼 많은 conv layer가 필요하다는 단점이 있는 반면 각 conv layer의 output을 parallel하게 도출할 수 있다는 장점이 있습니다. Self-attention은 이 둘의 단점들을 모두 극복한 셈으로, 긴 sequence도 한 번에 parallel하게 처리할 수 있습니다. Memory를 많이 잡아먹는다는 단점이 있긴 하지만 GPU는 계속 발전하고 있기 때문에 sequenced input을 처리하기에는 self-attention이 더 나은 primitive라고 할 수 있겠습니다.
Comparison of sequence processing primitives
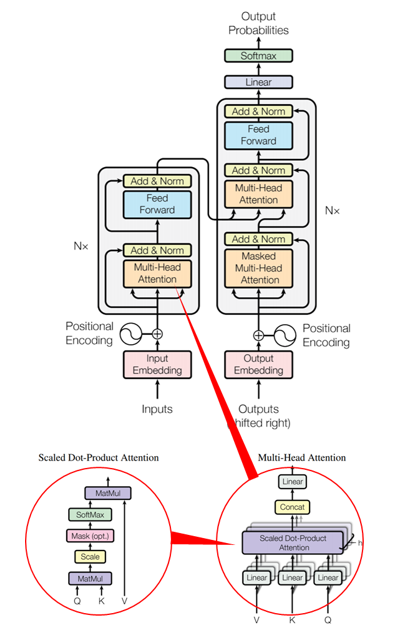
드!디!어! Transformer입니다. 앞서 말씀드린 “Attention is All You Need” (Vaswani et. al., NIPS 2017) 논문에서 소개된 network으로, encoder-decoder로 구성되어 있으며, encoder에 multihead self-attention layer, decoder에는 masked multihead self-attention layer, 그리고 encoder와 decoder 사이를 연결하는 multihead self-attention layer로 구성되어 있습니다. Input과 output은 word embedding과 positional embedding이 적용됩니다. Transformer 논문을 처음 보았을 때는 ‘무슨 소리를 하는건가’ 싶은 부분들이 좀 있었는데, attention mechanism의 발전 과정을 쭉 살펴보고 나서 보니 좀 더 잘 이해되지 않으신가요?
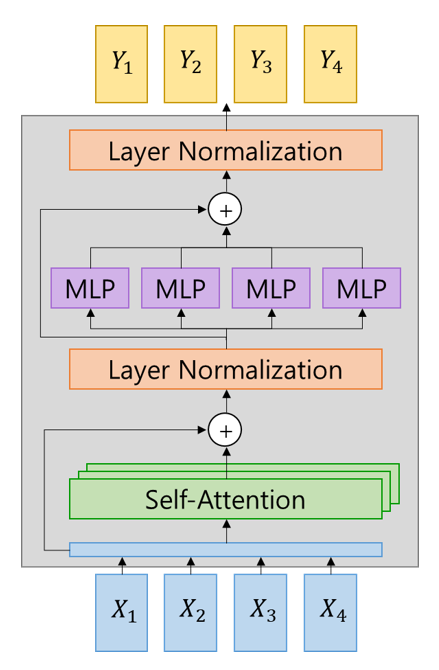
Encoder와 decoder를 구성하는 Transformer block을 다시 도식화해보면 다음과 같습니다. 이런 Transformer block을 겹겹이 쌓아서 하나의 Transformer 모델이 만들어지게 됩니다:
Vaswani et. al.의 논문에서는 encoder와 decoder에 각각 6개씩의 Transformer block을 사용했습니다. Encoder 및 decoder의 input dimension은 512였으며, 6 head 짜리 self attention layer를 사용했습니다.
NLP에 있어 Transformer 모델은 마치 Computer Vision에서 ImageNet이 나왔을 때와 같은 임팩트를 주었습니다. 이후 NLP는 인터넷 상의 수많은 text로 복잡한 Transformer를 pre-train 시켜놓은 다음, 각자의 task에 맞게 fine-tune 시키는 방식의 연구가 주를 이루었습니다 (물론 구현의 detail과 hyper-parameter는 다르겠지만요). 그리고 CNN 모델들이 복잡도를 더해가며 성능 arms race를 벌였던 것과 같은 일이 Transformer 쪽에서도 일어나게 됩니다. 돈으로 승부하는 quantitative expansion이…
- Transformers (Google):
- 12 layers, 8~16 heads, 65M params, 8x P100 (12hrs~3.5days)
- BERTs (Google):
- 12~24 layers, 12~16 heads, 110~340M params
- RoBERTa (Facebook):
- 24 layers, 16 heads, 355M params, 1024x V100 (1day)
- GPT-2's (OpenAI):
- 12~48 layers, 12~48 heads, 117M~1.5B params
- Megatron-LM's (Nvidia):
- 40~72 layers, 16~32 heads, 1.2~8.3B params, 512x V100 (9days)
- GPT-3's (OpenAI):
- 12~96 layers, 12~96 heads, 125M~175B params
- 355 years if trained on a single V100
국내에서도 여러 회사들이 GPT-3을 능가하는 hyperscale AI 모델을 만들겠다고 수천억원씩을 들여 param 수가 1조를 넘는 모델들을 만들겠다고 나섰다고 합니다. 뭐 그 중에는 비즈니스 도메인에 따라서 저런게 필요한 회사도 있는 것 같지만, 너무 다들 규모의 전쟁에만 집중하는 것이 아닌가 하는 생각도 드네요.