또 다시 ML의 큰 문제인 데이터에 대해 이야기하고, 이를 줄이기 위한 또 하나의 방법론에 대해 알아보도록 하겠습니다.
Transfer learning이라는 말을 여기저기서 들어보셨을 것입니다. ‘Pre-trained model로 신규 학습을 시작하는 것’ 이라고 알고 계시는 분들도 많을 것 같습니다. 보통 image classifier나 object recognizer를 만드는 경우, 학습 데이터를 구하고, 네트워크를 정하고 나면 이 네트워크를 ImageNet 등으로 학습시킨 pre-trained model을 찾는 것이죠. Pre-trained model을 사용하면 새로운 데이터로 모델이 학습하는 속도를 빠르게 해 주기도 하고, 특히 내 데이터가 모델을 학습시키기에 충분치 않은 경우라면 pre-trained model을 찾느냐 못찾느냐는 classifier의 성패를 좌우하게 될 수도 있겠죠.
실례를 들어 좀 다른 방향으로 이야기를 해보죠.
우리나라의 인공위성 중 아리랑 3호는 약 하루 2회 (주간, 야간) 한반도 상공을 지나며 고해상도 전자광학카메라로 사진을 촬영해왔습니다. 기상, 군사 등 다양한 목적을 가지고 다량의 사진을 찍었을 텐데요, 70cm급 해상도를 가지고 있다고 하니 촬영된 물체가 무엇인지 육안으로도 어느정도는 확인이 가능할 것 같긴 합니다만, 그래도 명확치 않은 것들도 있고 워낙 사진의 양이 많으니 object recognizer를 만들어서 자동으로 분류시키기로 하였습니다. 비용과 시간을 들여서 detect하고자 하는 object들에 대해 수많은 optical image들에 대한 annotation 작업을 마쳤습니다. 이제 위성에서 사진을 보내오면 자동으로 물체를 인식하여서 비구름이 어떻게 움직이는지 알아 강수를 예측하고, 북한의 어떤 함정이 몇 대 어느 항구에 정박해 있는지 알아 자동으로 국군의 준비태세를 갖추게 되었습니다.
그런데 optical camera에는 커다란 단점이 있었는데요, 이름대로 optical하기 때문에 빛이 없거나 가리면 촬영할 수가 없다는 점입니다. 하루에 2회 한반도 상공을 촬영할 수 있는데 구름이 끼어 있으면 지상 촬영이 안된다거나, 야간의 경우 촬영한 이미지로 지상의 object 관찰이 어렵다는 취약점이 있었습니다. 이러한 단점을 극복하고자 위성에서 지상에 레이다파를 쏘고, 다양한 굴곡면에 반사되어 나온 레이다파의 시차를 이용하여 해당 굴곡면을 가진 object의 형태를 파악하는 합성개구레이다 (Synthetic Aperture Radar, SAR) 기술을 개발, 차기 위성인 아리랑 5호와 아리랑 3A에 탑재하였습니다. 더이상 빛의 유무와 occlusion에 제약이 없어져서 밤에도, 구름낀 날에도 지상의 object 관찰이 가능해졌습니다. 그런데 바뀐 입력 이미지에서 object recognition을 돌리려니 SAR 이미지로 모델을 새로 학습해야 합니다. 여기서 문제가 발생합니다. 사람의 눈과 유사한 방식으로 동작한 optical image는 그 결과물도 우리가 인식하는 것과 유사한 반면, SAR은 그렇지가 않습니다. 아래는 optical과 SAR로 촬영한 각종 전술차량의 그림인데요, SAR 촬영 object를 눈으로 구분하는 것이 쉽지 않습니다.
모델 재학습을 하기로 결정하였습니다. 학습 데이터를 모으고 annotation을 달면 되는데, 극소수의 전문가 외에는 SAR 이미지를 식별조차 할 수 없어서 annotation을 달기가 어렵습니다. 예상 비용은 작업 시간은 무한정 늘어 갑니다. Active learning이든 뭐든 비용과 시간만 아낄 수 있다면 어떤 방법이라도 좋습니다. 마음 한 켠에는 작년에 거금을 들여 아리랑 3호의 optical image로 annotation을 달아 만들어두었던 학습 데이터가 아까와 죽겠습니다. 이걸 어떻게 써먹을 방법은 없는걸까요?
서론이 길었습니다만 오늘의 주제인 domain adaptation이 이런 경우의 문제를 해결해 줄 수 있는 한 방법입니다. 우선 문제를 formalize 하는 것부터 설명을 시작하겠습니다. 그러면서 transfer learning과 domain adaptation이 어떤 차이가 있는지도 이야기를 해보도록 하겠습니다.
문제가 정의되는, 혹은 데이터가 정의되는 도메인 $\mathcal{D}$는 $\mathcal{d}$ 차원을 가지는 데이터 $\mathcal{X}$와 그 확률분포 $P(\mathcal{X})$로써 다음과 같이 정의됩니다:
$\mathcal{D}={\mathcal{X}, P(\mathcal{X})}$
$\mathcal{X}$의 특정 set인 $X={x_1, x_2, …, x_n}\in\mathcal{X}$의 label을 $Y={y_1, y_2, …, y_n}\in\mathcal{Y}$라고 할 때, task $\mathcal{T}$를 입력 $X$가 $Y$의 확률을 가질 경우를 나타내는 조건부 확률인 $P(Y \mid X)$ 라고 정의할 수 있습니다.
도메인 적응(Domain Adaptation, DA)은 task(예를 들면 앞에서의 object recognition)의 domain이 모델을 학습했던 것(source domain, 예를 들면 optimal image domain)에서 어느정도 관련은 있지만 동일하지는 않은 다른 도메인(target domain, 예를 들면 SAR image domain)으로 변경되었을 때, source domain에서 학습된 knowledge를 transfer 해 주어 target domain에서 이용할 수 있도록 해줍니다. 계속해서 formalization 보시죠.
앞에서의 domain과 task 정의를 이용하여 source와 target의 domain과 task를 다음과 같이 표현할 수 있습니다:
Source domain: $\mathcal{D^S}={\mathcal{X^S}, P(\mathcal{X^S})}$, source task: $\mathcal{T^S}={\mathcal{Y^S}, P(Y^S \mid X^S)}$
Target domain: $\mathcal{D^T}={\mathcal{X^T}, P(\mathcal{X^T})}$, target task: $\mathcal{T^T}={\mathcal{Y^T}, P(Y^T \mid X^T)}$
우리가 일반적으로 모델을 학습시키는 경우에는 training과 test 사이에 task도 변하지 않고, 하나의 domain에 속한 데이터셋을 training과 test 셋으로 나누어 사용하기 때문에 $\mathcal{D^S}=\mathcal{D^T}$, $\mathcal{T^S}=\mathcal{T^T}$ 라고 할 수 있겠습니다. 그럼 위에서 얘기한 optical vs SAR image data의 경우는 어떨까요? 이 경우는 object recognition이라는 task는 변하지 않았지만 data의 domain은 optical에서 SAR로 바뀌었다고 볼 수 있기 때문에 $\mathcal{D^S} \neq \mathcal{D^T}$, $\mathcal{T^S}=\mathcal{T^T}$ 라고 할 수 있겠습니다. 이런 식으로 $\mathcal{D^S}=\mathcal{D^T}$, $\mathcal{T^S} \neq \mathcal{T^T}$ 인 경우도 있겠지요? 각각의 경우를 좀 더 general하게 구분해보겠습니다.
1. Same domain, same task
$\mathcal{D^S}=\mathcal{D^T}$, $\mathcal{T^S}=\mathcal{T^T}$
앞서 설명한대로 일반적인 ML 문제의 경우입니다. 주어진 데이터를 training과 test로 나눠서 학습하고 infer하면 됩니다.
2. Different domain, different task
$\mathcal{D^S} \neq \mathcal{D^T}$, $\mathcal{T^S} \neq \mathcal{T^T}$
아.. 생각만 해도 제일 골치아픈 경우입니다. 이런 문제를 과연 풀 수 있을까요.. Source와 target domain이 완전히 다른 경우는 knowledge transfer를 한다는 것 자체가 말이 안되고, 다르긴 하지만 어느정도 유사성이 있어야 합니다. Task의 경우도 마찬가지입니다. 구분을 하자면 inductive transfer learning 이나 unsupervised transfer learning 에 속하는 문제들이겠지만, 이런 경우는 그냥 새로운 데이터로 재학습하는게 나을 것 같습니다. Self-taught learning 이라는 기법도 있지만 toy example에서 6-70% 정도 성능을 보였고, 이후 지속적으로 개선되지 않은 것 같습니다 (제가 모르는 것일 수도 있음). 여튼 이번에 다루고자 하는 topic이 아니므로 이정도에서 패쓰합니다.
3. Same domain, different task
$\mathcal{D^S}=\mathcal{D^T}$, $\mathcal{T^S} \neq \mathcal{T^T}$
Source domain의 데이터가 충분하고, target domain의 labeled 데이터가 어느정도 있다면 source domain에서 학습된 모델이 source domain 상에서의 성능을 유지하면서 target domain에서도 동작하도록 학습을 할 수 있습니다. ImageNet pre-trained 모델로 face recognition에 적용하는게 이런 경우의 예라고도 할 수 있겠습니다. Inductive transfer learning 또는 multi-task learning 정도로 구분지을 수 있겠네요. 이 부분도 일단 out of topic입니다.
4. Different domain, same task
$\mathcal{D^S} \neq \mathcal{D^T}$, $\mathcal{T^S}=\mathcal{T^T}$
이게 바로 오늘 이야기를 하고자 하는 DA 입니다. 도메인을 다음과 같이 정의하였죠: $\mathcal{D}={\mathcal{X}, P(\mathcal{X})}$. DA를 좀 더 세분하자면 data source 자체가 다른, 그러니까 $\mathcal{X^S} \neq \mathcal{X^T}$ 때문에 $\mathcal{D^S} \neq \mathcal{D^T}$가 되는 경우를 heterogeneous DA 라고 하고, data source 자체는 같지만 ($\mathcal{X^S} = \mathcal{X^T}$) 그 분포가 달라서 ($P(\mathcal{X^S}) \neq P(\mathcal{X^T})$) $\mathcal{D^S} \neq \mathcal{D^T}$가 되는 경우를 homogeneous DA 라고 합니다. Optical vs SAR object recognition는 식별하고자 하는 object는 동일하나, 촬영 기법의 변화로 인해 해당 object를 나타내는 데이터(이미지)의 분포가 달라진 경우이기 때문에 homogeneous DA 로 구분됩니다. 특히 후자에 집중해서 볼 예정인데요, 이러한 종류의 DA가 실제 field에서 가장 빈번하게 요구될 것 같기 때문입니다.
데이터 측정 장비를 교체하는 경우(예: 광학카메라에서 레이더로, MRI에서 CT로)나 데이터의 분포가 변경되는 경우(예: 국내에서 학습한 자율주행시스템을 미국에 출시) 등이 homogeneous DA 를 적용할 수 있는 use case들이 될 것 같습니다. 여러 논문들에 나온 실험들에는 ‘webcam 이미지와 DSLR 이미지를 사용한 object recognition’, ‘실사와 합성 이미지를 사용한 드론 detection’, ‘하나의 빅데이터의 object annotation을 이용해 다른 빅데이터 object annotation 달기’, ‘USPS 숫자데이터와 MNIST를 이용한 손글씨 숫자인식’ 등과 같은 문제들도 다루고 있습니다.
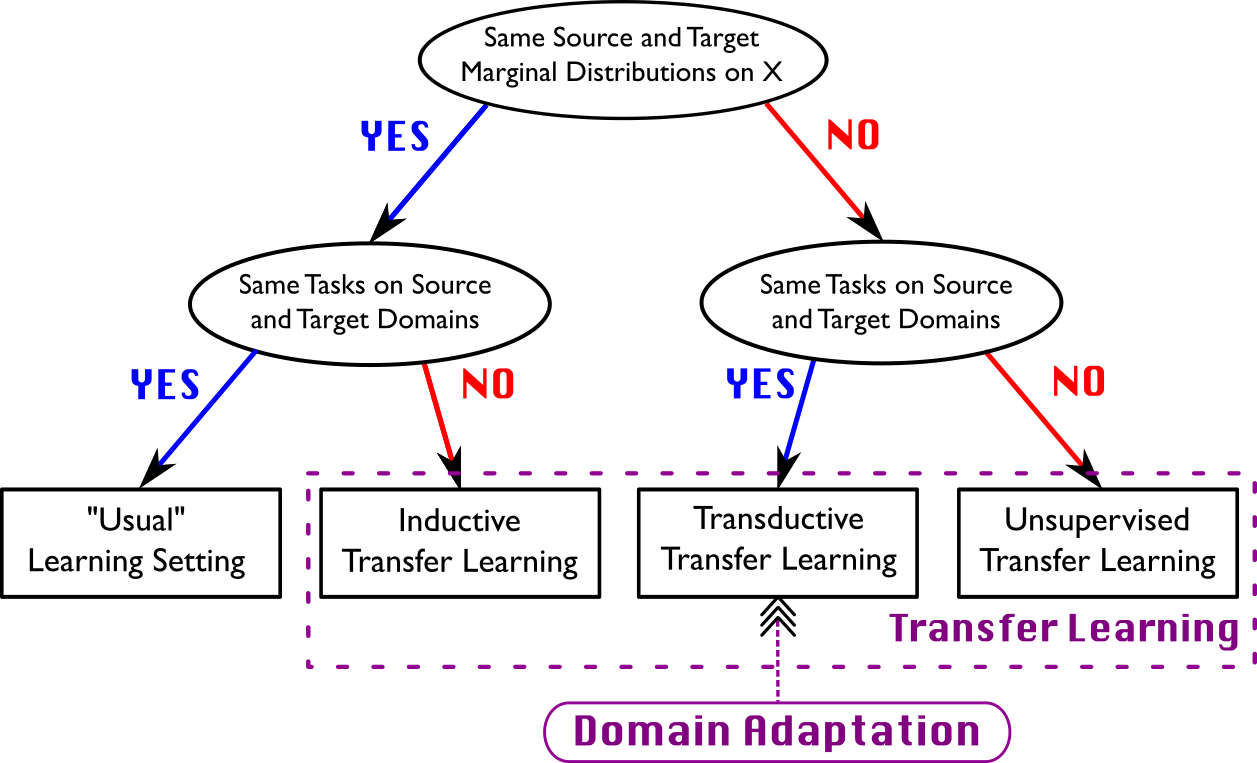
(일반적으로 말하는 Transfer learning (전이학습) 이란 위의 2, 3, 4번, 그러니깐 한 도메인에서 학습된 knowledge를 다른 도메인에 적용하거나, 한 task에 대해 학습한 knowledge를 다른 task에 적용하거나, 혹은 둘 다 동시에 하는 경우를 모두 일컫는 말입니다.)
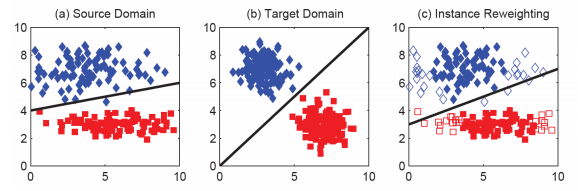
Homogeneous DA 문제를 해결하기 위한 수많은 연구가 있어왔습니다. Deep vs Shallow learning에서처럼 DA도 Deep 모델과 shallow 모델이 있는데 shallow model은 후다닥 넘기기로 하죠. Source와 target task를 둘 다 만족하도록 data instance의 weight를 조정하여 decision boundary를 바꿔주는 instance re-weighting method (아래 그림), perturbation function을 이용해서 점차적으로 decision boundary를 변경하는 adaptive-SVM 등의 parameter adaptation method 등과 같은 방법들이 shallow homogeneous DA 의 몇가지 예입니다.
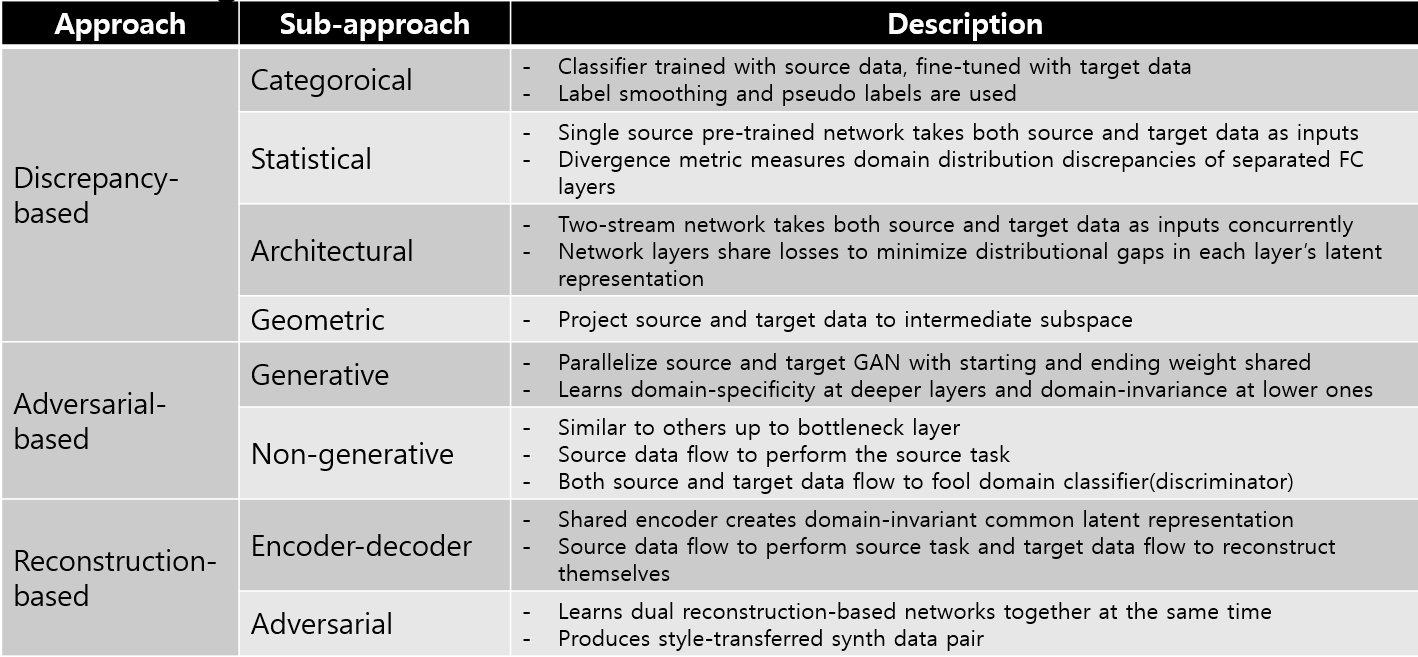
최근에는 deep neural network를 활용한 방법들이 사용되고 있으며, 리뷰 논문들에서는 접근 방식에 따라 discrepancy-based , adversarial-based , 그리고 reconstruction-based 의 큰 세 갈래로 구분하고 그 안에서 또 카테고리를 나누어 세분화하고 있습니다. 각 방식들의 대표적인 네트워크를 이용하여 하나씩 간략하게 살펴보겠습니다.
(유사도가 너무 다른 domain간에는 intermediate domain을 정의해서 DA를 조금씩 해 나가는 multi-step 방식도 있으나, 여기서는 domain간 어느정도의 유사성이 있다고 전제하고 one-step DA에 대해서만 고려합니다.)
Discrepancy-based
서로 다른 domain에 속한 $\mathcal{X^S}$와 $\mathcal{X^T}$의 분포간 divergence criteria를 줄임으로써 두 domain을 다 커버하는 하나의 모델을 만들겠다는 아이디어입니다. 결국 이 모델은 domain-invariant한 feature representation을 배우게 될 것이고, $\mathcal{X^S}$와 $\mathcal{X^T}$ 모두에 대해 좋은 성능을 내게 될 것입니다. 두 데이터 분포의 divergence를 줄이는 데에는 class (label) 정보, 두 데이터의 통계적인 분포, 네트워크 모델의 특성, 두 데이터의 기하학적인 구조를 활용하는 방법들이 있습니다.
Discrepancy-based: Categorical
Data의 class label을 discrepancy의 기준으로 사용하는 방식으로,
- $\mathcal{X^S}$와 $\mathcal{X^T}$ 모두 label이 달려있는 경우,
두 domain의 class들 간의 관계성을 유지하기 위해 soft label loss를 사용한다던가 (일반적인 경우에 class간 구분을 maximize하는 softmax loss를 쓰는데, 이러면 너무 한 domain 내에서의 class 구분에만 모델이 최적화되어버릴 수가 있습니다), 두 도메인의 동일 class 데이터는 가깝게 만들면서 다른 class 데이터 간의 거리는 멀게 만드는 embedding metric을 학습시키는 (어디서 많이 본 내용이지요, 지난 ArcFace 포스트에서 다루었던 내용과 같은 개념입니다) 방법 등이 있습니다. - $\mathcal{X^T}$의 class label이 없는 경우,
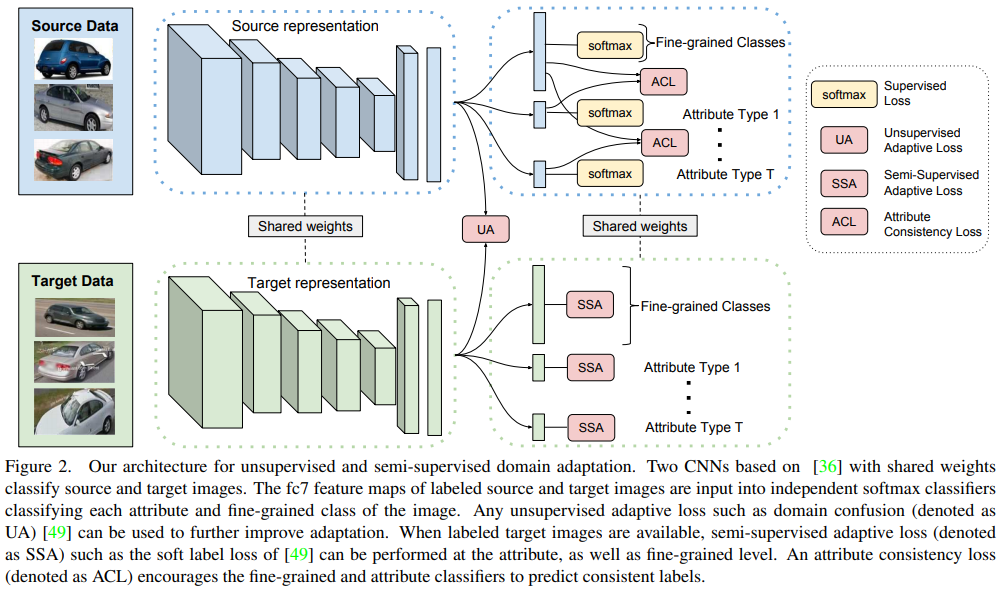
$\mathcal{X^T}$의 class label이 일부만 존재하는 경우에는 attribute 마다 softmax layer를 붙여서 category level loss와 각 attribute level loss를 조합해서 사용하는 multi-task DA 방식도 있고, $\mathcal{X^T}$ class label이 아예 없는 경우에는 $\mathcal{X^S}$로 학습시킨 모델에 unlabeled $\mathcal{X^T}$를 넣어서 class posterior probability를 구한 뒤, 이를 $\mathcal{X^T}$의 class label로 넣고 모델을 재학습시키는 pseudo-label 방식 등이 가능합니다 (pseudo-label에 대해선 여기 참조). 아래 그림은 multi-task DA architecture의 예시입니다. 설명이 길어지니 caption을 그대로 올리고, 논문도 링크합니다.
Discrepancy-based: Statistical
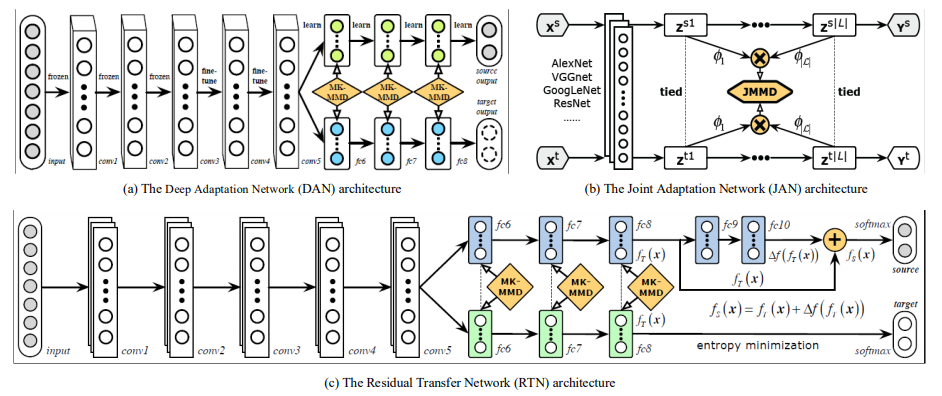
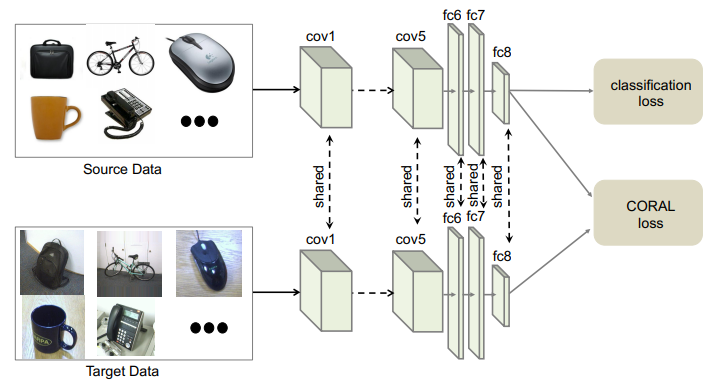
앞서 categorical 방식이 양 domain 데이터의 class label을 이용하여 divergence를 맞춰주려 했던 반면, 보다 근본적으로 domain의 data distribution discrepancy를 최소화하여 unsupervised 방법으로 domain-invariant feature representation을 학습하겠다는 것이 statistical 접근 방식입니다. 이 방식에서 사용되는 대표적인 discrepancy metric 중에는 MMD(maximum mean diiscrepancy) 및 그 variant들과 CORAL(correlation alignment)이 있습니다. MMD는 두 data sample이 동일한 probability distribution에서 추출한 것인지를 테스트하는 metric으로, 데이터 샘플을 재생핵 힐베르트 공간(reproducing kernel Hilbert space, RKHS)이란 곳으로 매핑시킨 후 평균을 비교하는 방식으로 동작합니다. 더 자세히 알고싶으신 분들을 위해 링크 남깁니다. 간단히 말하면 (RKHS로 사영한 후의) mean이 가까우면 distribution도 같을 가능성이 높다는 의미입니다. 더 간단히 하면 두 distribution의 similarity measure라고 보셔도 될 것 같습니다. MMD가 크면 mean discrepancy가 크다는 말이니까 distribution도 다르겠지요? 그러니깐 MMD loss를 두고 이걸 최소화시키도록 네트워크를 학습하면 source와 target distribution이 가까와지게 되고, 이는 결국 domain-invariant한 feature representation을 배울 수 있다는 말이 됩니다. 아래 그림은 MMD를 사용하여 DA를 수행하는 모델의 몇가지 예입니다. DAN (Domain Adaptation Network)의 예를 보면 $\mathcal{X^S}$를 네트워크에 넣어서 conv layer를 통과시킨 후 여러개의 kernel로 구성된 “adaptation layer”를 지나 class를 출력하도록 학습합니다. 이렇게 학습된 네트워크에 $\mathcal{X^T}$를 입력하는데, 이번엔 conv layer 이후 다른 adaptation layer path를 타게끔 하면서, $\mathcal{X^S}$와 $\mathcal{X^T}$의 매 kernel단 출력값들의 MMD loss를 계산하여 domain-invariance를 학습시키는 방식입니다. CORAL에서의 loss는 두 분포의 공분산간의 L2-distance로, 공분산을 일치시켜 domain-invariance를 학습하게 하는 것입니다 (링크). 두 번째 아래 그림은 CORAL loss를 딥 네트워크에 적용시킨 예입니다. Labeled $\mathcal{X^S}$로 classification loss를 학습하면서, weight를 공유하는 parallel network를 구성하여 unlabeled $\mathcal{X^T}$를 집어넣고, 두 네트워크의 FC8 layer의 activation 값으로 공분산을 구해 CORAL loss를 계산하였습니다.
포스팅이 너무 길어져서 반으로 나누겠습니다 ^^; Part2는 하루이틀 후에 올릴게요.
논문링크 (survey 논문 위주 리스트업):
A Survey on Transfer Learning
Domain Adaptation for Visual Applications: A Comprehensive Survey
Deep Visual Domain Adaptation: A Survey
Recent Advances in Transfer Learning for Cross-Dataset Visual Recognition: A Problem-Oriented Perspective