오늘은 triplet을 이용한 FaceNet 이후의 xxxFace 시리즈에 대해 이야기를 해보려고 합니다. 양이 많습니다!
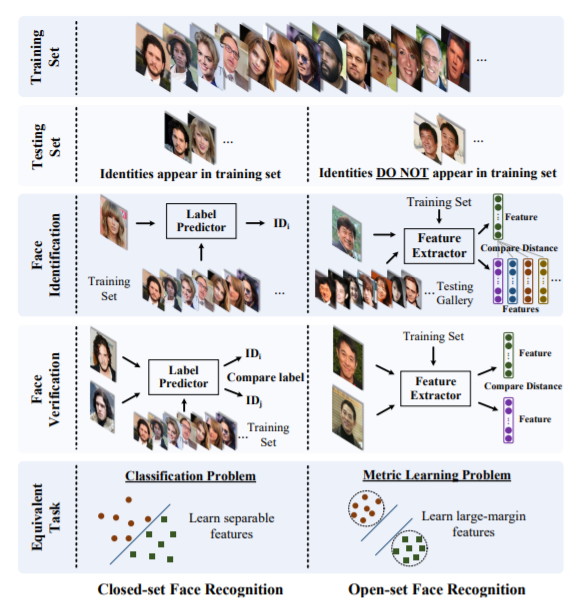
FaceNet에 대한 지난포스트에서 open-set face recognition에 대한 문제를 이야기했습니다. 일반적인 classification의 경우 각 class에 assign된 data로 모델을 학습하고, unseen test data를 어느 class에 할당할 것인지를 결정합니다. 이런걸 closed-set 문제라고 합니다. 하지만 지난 포스트에서 언급했던 face recognition과 같은 경우 학습되지 않은 얼굴을 어떻게 인식할 것인지의 문제가 생깁니다. 할당할 class가 없기 때문에 FaceNet에서는 probe face를 gallery에 있는 얼굴들과 비교하기 위한 low-dimensional embedding을 triplet을 구성하여 학습시켰던 것을 기억하실 것입니다. 이런걸 open-set 문제라고 하는데요, 결국 open-set face recognition은 ‘real domain에서 다른 얼굴이라면 feature space에서도 다른 얼굴이라고 인식하는’것을 학습하는 것이고, 다르게 표현한다면 face image를 feature space로 mapping하기 위한 metric을 학습하는 문제라고 할 수 있습니다. 이 feature space는 서로 다른 얼굴들에 대한 구분력을 최대화해야 할 것이므로 discriminative margin을 최대화하는 방향으로의 mapping metric을 배워야 합니다.
Discriminative feature를 효과적으로 배워보자는 두 가지 시도가 우선 있었습니다.
Contrastive Loss
Contrastive loss(또는 pairwise ranking loss)는 anchor-positive, anchor-negative pair를 구성해서 각 이미지를 Siamese network에 집어넣어 나온 feature들을 이용하여 다음의 loss를 최적화하게 됩니다:
$L_{contrastive} = (1-Y) \frac 1 2 (\Vert f(x^i) - f(x^j) \Vert)^2 + Y \frac 1 2{max(0, m - \Vert f(x^i) - f(x^j) \Vert)}^2$
$Y$: 바이너리 label (anchor-positive이면 0, anchor-negative이면 1)
$f(x^i)$: anchor sample
$f(x^j)$: positive 또는 negative sample
위 식에서 $f(x^i) \approx f(x^j)$ 이면 (anchor-positive set이란 얘기겠죠) $Y$의 값이 0이 되어서 위 loss 식의 앞 항만 남게 되며, anchor-positive 간의 닮은 정도만큼 $(\Vert f(x^i) - f(x^j) \Vert)^2$의 값이 작아져서 최종 loss는 Mean Squared Error (MSE)와 거의 같아집니다. 그 반대로 anchor-negative의 경우에는 loss 식의 뒷 항만 남게 되고, 이 때에도 마찬가지로 anchor-negative의 닮은 정도만큼 $(\Vert f(x^i) - f(x^j) \Vert)^2$의 값이 작아지긴 하지만 차이가 작으면 작을수록 loss값은 $\frac 1 2 m^2$에 근접하게 됩니다. 이렇게 m이 anchor-negative pair에 대한 margin 역할을 하는거죠.
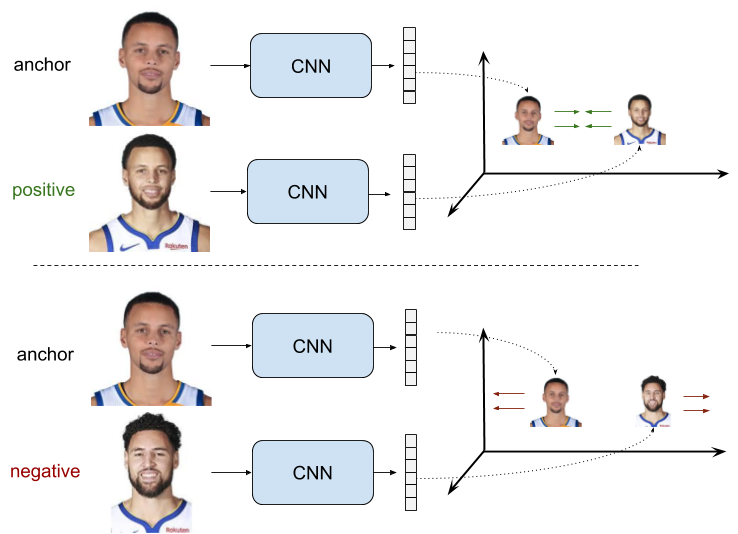
FaceNet 의 Triplet Loss
Triplet loss에 대해서는 지난 포스트에서 설명드린 바 있습니다. $d(A, P) < d(A, N) < d(A, P)+\alpha$ 조건을 추가하여서 discriminative power를 좀 더 강화하였죠.
SphereFace 의 Angular Loss
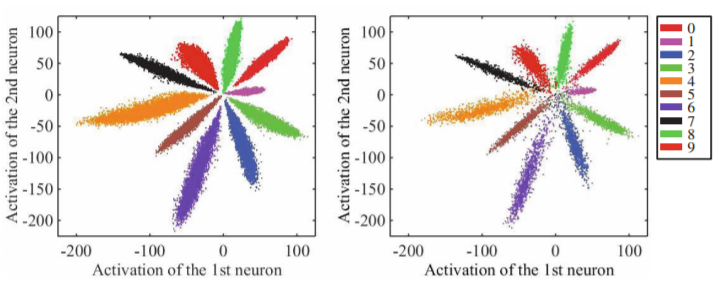
Contrastive와 triplet loss 모두 기존의 softmax loss를 개선하여 latent representation의 discriminativeness를 강화하고 이에 따른 margin을 추가로 학습하였지만, 여전히 Euclidean space에서의 distance를 기준으로 데이터의 멀고 가까움을 계산하였다는 점은 변하지 않았습니다. Center loss를 정의한 논문에서 MNIST 데이터로 softmax 기반 classifier를 학습하고 1st, 2nd layer activation을 plot해 본 결과에서도 나타났지만, 이후 CASIA face dataset을 softmax 및 normalized softmax (modified softmax) 기반으로 학습한 feature를 plot해 본 결과 이 feature들이 angular한 특성을 가지고 있다는 것을 관찰하고, 자연히 Euclidean이 아닌 Euler space에서의 distance 기반 margin을 찾아보게 되었습니다.
아래 그림을 보시면 CASIA face dataset을 사용, (1) classifier를 softmax로 학습한 feature를 Euclidean space에 plot한 것; (2) (1)을 Euler space에 plot; (3) modified softmax (normalized)로 학습한 feature의 Euclidean plot; (4) (3)의 Eulerian plot; (5) angular softmax로 학습한 feature의 Euclidean plot; (6) (5)의 Eulerian plot 을 잘 보여주고 있습니다. 각 Euclidean plot에는 decision boundary가 x=0 으로 나와있고, Eulerian plot들에는 angular bisector가 별도로 표시되어 있습니다. Euclidean보다 Eulerian의 intra-class compactness 및 intra-class dispension이 더 크고, 그 중에서도 angular softmax를 사용한 (6)의 class간 discriminitive power가 가장 크다는 것을 확인할 수 있습니다.
SphereFace의 A-Softmax 식은 다음과 같습니다:
$L_{SphereFace} = -\frac 1 N \sum_i log(\frac {e^{\Vert x_i \Vert cos(m\theta_{y_i}, i)}} {e^{\Vert x_i \Vert cos(m\theta_{y_i}, i)+\sum_{j \neq y_i}e^{\Vert x_i \Vert cos(\theta_j, i)}}})$
CosFace 의 Angular Loss
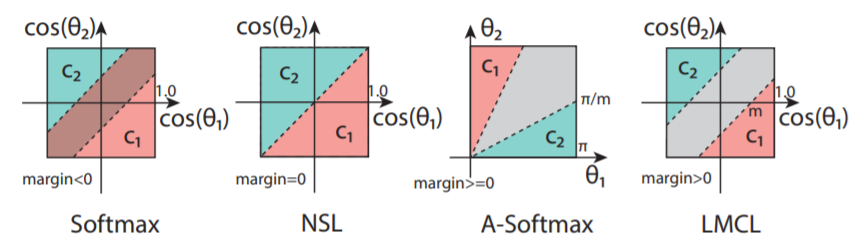
SphereFace가 각도 값에 곱으로 margin (multiplicative angular margin, 위 식의 $\theta$ 앞에 붙은 $m$)을 주었는데요, 이 decision boundary는 아래 그림의 3번째 ‘A-Softmax’와 같이 Euler space에서의 vector로 표시될 수 있습니다 (위 그림의 (6)과 동일한겁니다). A-Softmax의 경우 $\Vert \theta_1 - \theta_2 \Vert$ 값에 따라 회색으로 표시된 decision margin이 변한다는 점 때문에, C1과 C2가 유사하다면 (얼굴이 비슷하다면) margin이 작아지는 단점이 있었습니다. 또한 gradient 계산을 용이하게 하기 위해 A-Softmax의 $m$은 정수여야 한다는 큰 단점이 있었습니다. Margin이 큰 값으로 변경되기 때문에 모델을 수렴시키기 어렵게 된 것이죠. Class similarity와 무관하게 constant한 margin을 보장해주고, 수렴을 위해 기존 softmax loss의 도움이 필요없도록 additive angular margin을 주는 loss를 만든 것이 CosFace입니다 (아래 그림의 Large Margin Cosine Loss, LMCL).
CosFace의 LMCL formula입니다. LMCL의 additive angular margin을 SphereFace의 multiplicative angular margin과 비교해서 보시죠:
$L_{CosFace} = -\frac 1 N \sum_i log(\frac {e^{s(cos(\theta_{y_i}, i)-m)}} {e^{s(cos(\theta_{y_i}, i)-m)}+\sum_{j \neq y_i}e^{s(cos(\theta_j, i)-m)}})$
ArcFace 의 Angular Loss
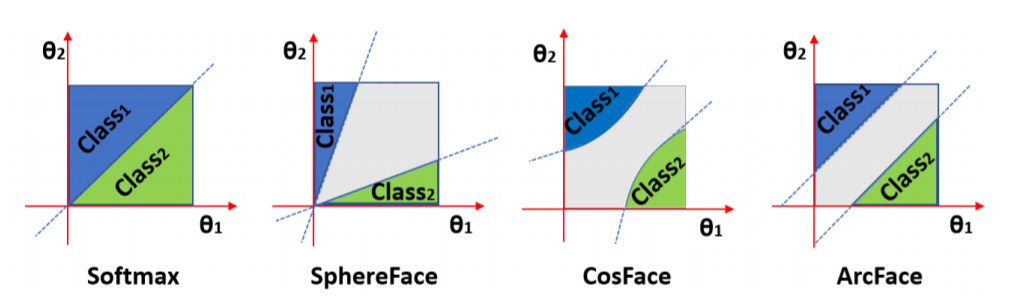
ArcFace는 additive cosine margin을 이용합니다 (CosFace는 additive angular margin이었죠). Logit에 $arccos$함수를 씌워서 similarity가 아닌 실제 angle (angular distance)을 뽑고, 여기에 margin penalty를 더한 후 $cos$함수로 logit을 복원하는 방식을 사용하여서 ArcFace라고 이름지었습니다. Normalized 된 hypersphere manifold 상에서 distance를 가지고 inter-class dispersion, intra-class compactness를 maximize하는 것이기 때문에 geodesic distance와 일치하는 angular margin을 사용한다는 점은 학습에 도움이 될 것입니다. 아래 angular plane에서의 decision boundary는 이와 같은 ArcFace의 장점을 보여줍니다. 앞서 보았던 decision margin과 비교해보면 CosFace의 경우 $cos\theta$를 axes로 놓고 그렸던 decision margin을 angular ($\theta$) plane에 그려보니 일정하지 않게 된 것을 볼 수 있습니다. 반면 ArcFace의 decision margin은 angle이 변함에 따라 constant 하지요.
ArcFace의 loss formula입니다. $cos$를 벗겨서 margin을 넣고 다시 $cos$를 씌워주었기 때문에 LMCL과 달리 additive margin이 $cos$함수 안에 들어있는 것을 볼 수 있습니다:
$L_{ArcFace} = -\frac 1 N \sum_i log(\frac {e^{s(cos(\theta_{y_i}+m))}} {e^{s(cos(\theta_{y_i}+m))}+\sum_{j=1,j \neq y_i}e^{scos\theta_j}})$
CASIA, LFW 등 다양한 face dataset에서 동일한 모델로 테스트한 결과 ArcFace는 기존 Euclidean space의 softmax기반 방식들보다도, angular space의 여타 솔루션들보다 더 좋은 성적을 거두었습니다 (더 많은 결과는 논문에서 확인).
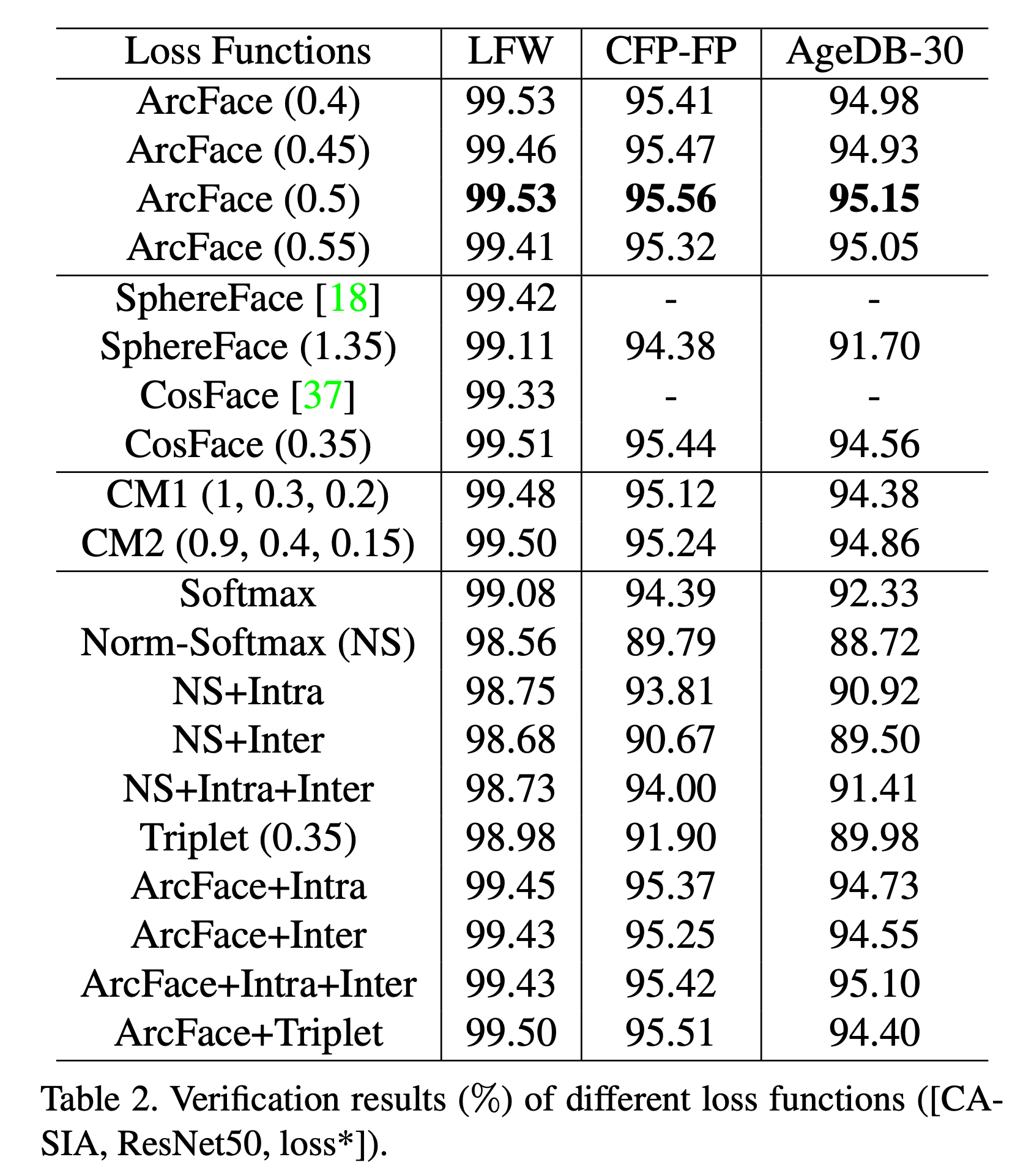
Normalize된 angular space에서 우수한 성능을 보이는 ArcFace는 scale-invariant, rotational-invariant한 특성 때문에 face 뿐만 아니라 다양한 image data의 open-set recognition에 활용이 가능할 것 같습니다. 마침 EstSoft에서 ArcFace로 Kaggle competition에 입상했다는 글도 있네요 (링크).
최근에 나온 CurricularFace까지 언급하면서 curriculum learning 이야기를 시작해놓을까 했는데 너무 길어지네요. 다음을 기약합니다.
논문링크:
SphereFace
CosFace
ArcFace
CurricularFace